suivant : 1.23.3.1 En pratique remonter : 1.23 Techniques d'intégration précédent : 1.23.2.1 Exemples

1.23.3 Changement de variable

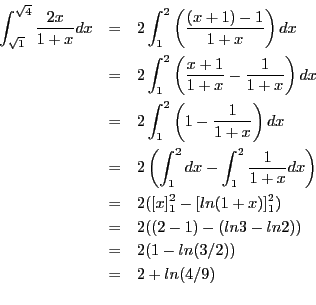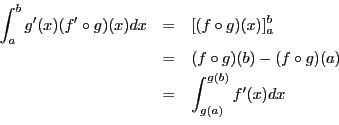
On remarque que

$$\begin{eqnarray*} \displaystyle \int_a^b g^{\prime}(x)(f^{\prime} \circ g)(x)d... ...\ &= & \displaystyle \int_{g(a)}^{g(b)} f^{\prime}(x)dx \\ \end{eqnarray*}$$

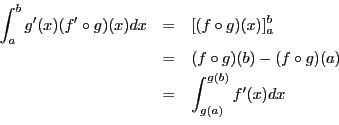
On en déduit que

$$\int_a^b g^{\prime}(x)(f^{\prime} \circ g)(x)dx = \int_{g(a)}^{g(b)} f^{\prime}(x)dx$$

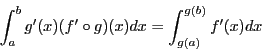
La difficulté est de trouver la fonction $g$. Par exemple, calculons

$$\int_1^4 \frac{1}{1 + \sqrt{x}}dx$$

Posons $g(x) = \sqrt{x}$, alors on a $$g^{\prime}(x) = \frac{1}{2\sqrt{x}}$$, comme $$g^{\prime}(x)f^{\prime}(g(x)) = \frac{1}{1 + \sqrt{x}}$$, alors on a

$$f^{\prime}(x) = \frac{2x}{1 + x}$$

Utilisons la formule ci-dessus :

$$\int_1^4 \frac{1}{2\sqrt{x}}\frac{2\sqrt{x}}{1 + \sqrt{x}}dx = \int_{\sqrt{1}}^{\sqrt{4}} \frac{2x}{1 + x}dx$$

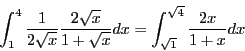
Cette intégrale est bien moins difficile à résoudre :

$$\begin{eqnarray*} \displaystyle \int_{\sqrt{1}}^{\sqrt{4}} \frac{2x}{1 + x}dx ... ...ystyle 2(1 - ln(3/2)) \\ &= & \displaystyle 2 + ln(4/9) \\ \end{eqnarray*}$$