



suivant : 1.24 Développements limités
remonter : 1.23.3 Changement de variable
précédent : 1.23.3.1 En pratique
Cherchons la primitive de
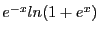 qui s'annule en
qui s'annule en 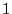 ,
cela revient à calculer l'intégrale
,
cela revient à calculer l'intégrale
Posons 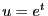 , si
, si 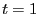 alors
alors 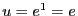 , si
, si 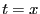 , alors
, alors 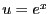 .
On a
.
On a
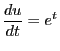 , d'où
, d'où
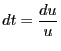 . Donc
. Donc
en intégrant par parties, on a
on simplifie,
Décomposons
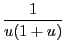 en éléments simples :
déterminons
en éléments simples :
déterminons 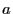 et
et 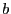 tels que
tels que
Il vient 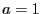 et
et 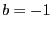 , d'où
, d'où
On en déduit,
ce qui nous donne
D'ou,
en simplifiant, on a
klaus
2011-02-14
![]() qui s'annule en
qui s'annule en ![]() ,
cela revient à calculer l'intégrale
,
cela revient à calculer l'intégrale
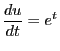 , d'où
, d'où
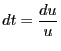 . Donc
. Donc
![\begin{displaymath}\int_e^{e^x} \frac{ln(1 + u)}{u^2}du = \left[\frac{-1}{u}ln(1...
...)\right]_e^{e^x} - \int_e^{e^x} \frac{-1}{u} \frac{1}{1 + u} du\end{displaymath}](img1168.png)
![\begin{displaymath}\int_e^{e^x} \frac{ln(1 + u)}{u^2}du = -\left[\frac{ln(1 +
u)}{u}\right]_e^{e^x} + \int_e^{e^x} \frac{1}{u(1 + u)} du\end{displaymath}](img1169.png)