suivant : 1.6.2.4 Produit de deux remonter : 1.6.2 Opérations sur les précédent : 1.6.2.2 Multiplication par un

1.6.2.3 Transposition

Etant donnée une matrice $A$ de dimensions $n \times p$, la transposée de $A$, notée $A^t$, est une matrice $p \times n$ telle que $\forall i \in \{1, \ldots, n\}, \forall j \in \{1, \ldots, p\}$,

$$a^t_{ij} = a_{ji}$$

Autrement dit, on transpose une matrice en la retournant comme une crêpe autour de l'axe formé par la diagonale :

$$A^t = \left( \begin{array}{l l l l l} a_{11} & \ldots & a_{... ...} & \ldots & a_{jn} & \ldots & a_{pn} \\ \end{array} \right)$$

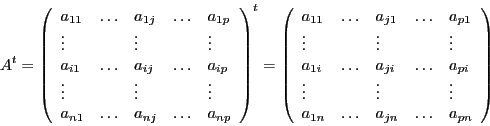
Par exemple, si 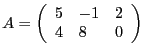$A = \left( \begin{array}{l l l} 5 & -1 & 2\\ 4 & 8 & 0\end{array}\right)$, alors

$$A^t = \left( \begin{array}{l l l} 5 & -1 & 2\\ 4 & 8 & 0\e... ...( \begin{array}{l l} 5 & 4\\ -1 & 8\\ 2 & 0\end{array}\right)$$

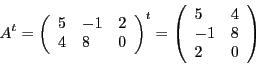
Une matrice égale à sa transposée est une matrice symétrique.