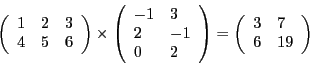Etant données deux matrices ![]() et
et ![]() de dimensions respectives
de dimensions respectives ![]() et
et ![]() , le produit de
, le produit de ![]() par
par ![]() est une matrice
est une matrice
![]() de dimensions
de dimensions ![]() vérifiant :
vérifiant :
![]() ,
,
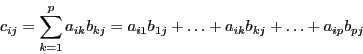
Ne nous laissons pas impressioner par la complexité apparente de la
formule et faisons un joli dessin en considérant le cas particulier où
![]() , nous allons représenter le produit de
, nous allons représenter le produit de ![]() par
par ![]() de
la sorte :
de
la sorte :
Remplaçons ![]() ,
, ![]() et
et ![]() :
:
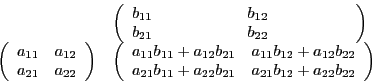
Observons : on a
![]() . Si l'on
extrait la première ligne de
. Si l'on
extrait la première ligne de ![]() et la première colonne de
et la première colonne de ![]() , on
obtient
, on
obtient
![]() et
et
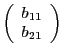 . On détermine
donc
. On détermine
donc ![]() d'abord en multipliant entre elles les premières
composantes de ces deux vecteurs, puis en faisant de même avec les
deuxième composantes. La valeur recherchée est la somme de ces deux
produits. Si par exemple, on a
d'abord en multipliant entre elles les premières
composantes de ces deux vecteurs, puis en faisant de même avec les
deuxième composantes. La valeur recherchée est la somme de ces deux
produits. Si par exemple, on a
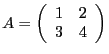 et
et
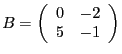 , alors
, alors
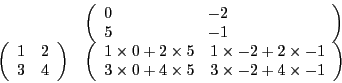
Ce qui nous donne
Notez bien que pour qu'il soit possible de multiplier deux matrices, il faut que le nombre de colonnes de la première soit égal au nombre de lignes de la deuxième. La matrice produit a alors autant de lignes que la première matrice et autant de colonnes que la deuxième. Observez maintenant l'exemple suivant, il vous est conseillé de vérifier si le résultat est juste (peut-être qu'une erreur s'est subrepticement glissée quelque part...).