



suivant : 1.3 Probabilités conditionnelles
remonter : 1.2.7 Équiprobabilité
précédent : Exercice 8 - Lancers
- Prouvez que
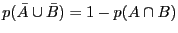 . Puis que
. Puis que
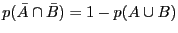 .
.
- Prouvez que si
 et
et  sont incompatibles, alors
sont incompatibles, alors
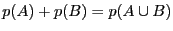 .
.
- Prouvez que si
 et
et  sont indépendants, alors
sont indépendants, alors
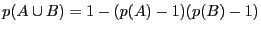 .
.
- Prouvez que si
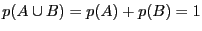 , alors
, alors 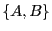 est
un système complet d'événements.
est
un système complet d'événements.
- Prouvez que
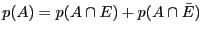 , vous
utiliserez le fait que
, vous
utiliserez le fait que
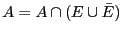 .
.
- Prouvez que si
 et
et  sont indépendants, alors leurs
complémentaires sont aussi indépendants.
sont indépendants, alors leurs
complémentaires sont aussi indépendants.
Alexandre
2009-05-26