



suivant: Exercice 1 - Exponentiation
monter: Terminaison
précédent: Fin de l'exemple
Table des matières
Déterminons un algorithme qui calcule le produit de deux entiers 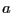 et
et 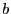 avec
avec 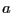 positif ou nul sans effectuer de multiplication.
positif ou nul sans effectuer de multiplication.
![\begin{algorithm}[H]
\dontprintsemicolon
$p \longleftarrow 0$\;
$m \longleftarro...
...$}
{
$p \longleftarrow p + b$\;
$m \longleftarrow m + 1$\;
}
\end{algorithm}](img73.gif)
- Montrons que le programme se termine. La séquence formée par les
valeurs prises par
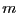 au fil des itérations est strictement
croissante, il y a donc un moment où
au fil des itérations est strictement
croissante, il y a donc un moment où  . Donc l'algorithme
se termine.
. Donc l'algorithme
se termine.
- Considérons comme invariant de boucle
 , montrons par
récurrence qu'il est vérifiée.
, montrons par
récurrence qu'il est vérifiée.
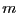 est
est 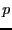 sont initialisés à
sont initialisés à 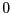 , on a bien
, on a bien  .
.
- montrons maintenant que la propriété est conservée. Supposons qu'au
début d'une itération donnée, on ait
 . Soient
. Soient  et
et  les valeurs de ces variables à la fin de cette
itération, montrons que l'on a
les valeurs de ces variables à la fin de cette
itération, montrons que l'on a
 . On a les
relations
. On a les
relations
 et
et
 . Donc
. Donc
 . La propriété est
donc conservée par chaque itération de l'algorithme.
. La propriété est
donc conservée par chaque itération de l'algorithme.
- La première de valeur de
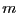 qui nous fera sortir de la boucle est
qui nous fera sortir de la boucle est
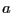 , donc après la dernière itération on aura
, donc après la dernière itération on aura  . Ce
programme place donc dans
. Ce
programme place donc dans 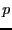 le produit de
le produit de 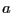 par
par 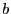 .
.
Sous-sections




suivant: Exercice 1 - Exponentiation
monter: Terminaison
précédent: Fin de l'exemple
Table des matières
klaus
2010-08-05
![]() et
et ![]() avec
avec ![]() positif ou nul sans effectuer de multiplication.
positif ou nul sans effectuer de multiplication.
![\begin{algorithm}[H]
\dontprintsemicolon
$p \longleftarrow 0$\;
$m \longleftarro...
...$}
{
$p \longleftarrow p + b$\;
$m \longleftarrow m + 1$\;
}
\end{algorithm}](img73.gif)