



suivant: Exercice 4 - Tri
monter: Un autre exemple
précédent: Exercice 2 - Plus
Table des matières
Nous allons écrire et démontrer la validité de l'algorithme du tri par
insertion. Nous rappelons que
![$T = [T_1, \ldots, T_n]$](img87.gif) est trié si
est trié si
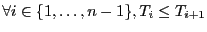 . Etant donné le
programme suivant :
. Etant donné le
programme suivant :
![\begin{algorithm}[H]
\dontprintsemicolon
\Procedure{$insere(T, k)$}
{
$i \lo...
...{
$echanger(T[i - 1], T[i])$\;
$i \longleftarrow i - 1$
}
}
\end{algorithm}](img91.gif)
Prouver que si on passe en paramètre à 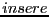 un tableau
un tableau 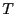 dont les
dont les
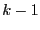 premiers éléments sont triés, alors à la fin de son exécution,
les
premiers éléments sont triés, alors à la fin de son exécution,
les  premiers éléments dont triés. Etant donné le programme suivant :
premiers éléments dont triés. Etant donné le programme suivant :
![\begin{algorithm}[H]
\dontprintsemicolon
\Procedure{$triInsertion(T[n])$}
{
\Pour{$i \in \{2, \ldots, n\}$}
{
$insere(T, i)$
}
}
\end{algorithm}](img95.gif)
Démontrer la terminaison et la validité de 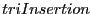 .
.
Voici le corrigé de la première question : L'algorithme se termine
bien car les valeurs prises par 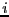 forment une séquence de nombres
entiers strictement décroissante. Si l'on ne sort pas de la boucle
avec
forment une séquence de nombres
entiers strictement décroissante. Si l'on ne sort pas de la boucle
avec
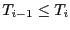 , on aura forcément
, on aura forcément 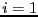 après la dernière
itération. Prenons comme invariant de boucle la conjonction des
conditions suivantes :
après la dernière
itération. Prenons comme invariant de boucle la conjonction des
conditions suivantes :
- La tranche
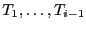 est triée
est triée
- La tranche
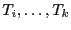 est triée
est triée
-
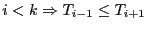
Prouvons cette propriété par récurrence :
- A la première itération, on a
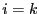 . Comme
. Comme
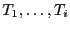 correspond à la tranche
correspond à la tranche
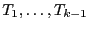 donc par
hypothèse cette tranche est triée. La tranche
donc par
hypothèse cette tranche est triée. La tranche
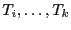 est réduite au seul élément
est réduite au seul élément 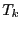 , elle est donc
nécessairement triée. Comme
, elle est donc
nécessairement triée. Comme 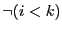 , la troisième
condition est trivialement vérifiée.
, la troisième
condition est trivialement vérifiée.
- Supposons qu'au début d'une itération arbitraire, les trois
propriétés soient vérifiées. Soient
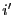 la valeur de
la valeur de
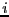 et
et 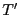 le tableau
le tableau 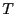 à la fin de cette
itération. Montrons alors que
à la fin de cette
itération. Montrons alors que
- La tranche
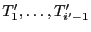 est triée
est triée
- La tranche
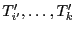 est triée
est triée
-
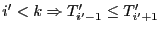
D'une part, on a 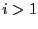 et
et
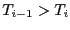 . Par ailleurs,
. Par ailleurs,
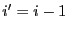 ,
,
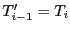 et
et
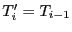 . Tous les autres éléments de
. Tous les autres éléments de 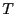 et de
et de 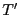 coïncident. Montrons les trois propriétés :
coïncident. Montrons les trois propriétés :
- Par hypothèse de récurrence, la tranche
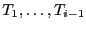 est triée, donc la tranche
est triée, donc la tranche
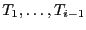 que l'on
obtient en ne comptabilisant pas le dernier élément est aussi
triée. Comme les éléments de
que l'on
obtient en ne comptabilisant pas le dernier élément est aussi
triée. Comme les éléments de 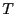 et
et 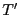 d'indices
différents de
d'indices
différents de 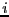 et
et 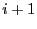 sont les mêmes et que
sont les mêmes et que
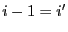 , alors
, alors
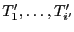 est triée.
est triée.
- Par hypothèse de réccurrence
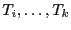 est triée,
en ne considérant pas le premier élément, on a
est triée,
en ne considérant pas le premier élément, on a
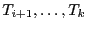 , comme les éléments de cette tranche
coïncident avec
, comme les éléments de cette tranche
coïncident avec 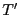 , alors
, alors
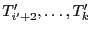 est triée. Par
ailleurs, on a
est triée. Par
ailleurs, on a
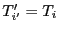 et
et
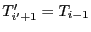 , comme
, comme
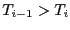 , alors
, alors
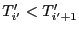 . Si
. Si 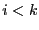 , alors par hypothèse de récurrence, on a
, alors par hypothèse de récurrence, on a
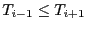 , donc
, donc
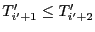 . Dans ce cas, on a
. Dans ce cas, on a
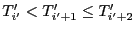 avec
avec
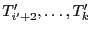 triée. Donc
triée. Donc
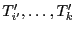 est triée. Si
est triée. Si 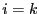 , alors la tranche
, alors la tranche
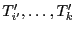 est réduite aux deux éléments
est réduite aux deux éléments
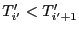 , elle est donc
triée.
, elle est donc
triée.
- Quelle que soit la valeur de
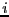 , on a nécessairement
, on a nécessairement
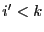 , il faut donc montrer que
, il faut donc montrer que
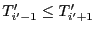 . Or
. Or
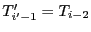 et
et
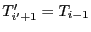 . Par hypothèse de récurrence,
. Par hypothèse de récurrence,
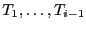 est triée, donc on a
est triée, donc on a
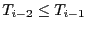 , d'où
, d'où
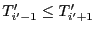 .
.
Après la denière itération, si 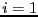 , alors la première tranche ne
contient aucun élément et la deuxième condition de l'invariant de
boucle permet de conclure que toute la tranche
, alors la première tranche ne
contient aucun élément et la deuxième condition de l'invariant de
boucle permet de conclure que toute la tranche
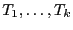 est
triée. Si par contre, on sort de la boucle parce que
est
triée. Si par contre, on sort de la boucle parce que
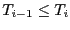 , alors comme, d'après l'invariant de boucle,
, alors comme, d'après l'invariant de boucle,
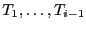 et
et
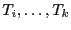 sont triées, alors
sont triées, alors
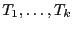 est triée.
est triée.




suivant: Exercice 4 - Tri
monter: Un autre exemple
précédent: Exercice 2 - Plus
Table des matières
klaus
2010-08-05
![\begin{algorithm}[H]
\dontprintsemicolon
\Procedure{$insere(T, k)$}
{
$i \lo...
...{
$echanger(T[i - 1], T[i])$\;
$i \longleftarrow i - 1$
}
}
\end{algorithm}](img91.gif)
![]() est trié si
est trié si
![]() . Etant donné le
programme suivant :
. Etant donné le
programme suivant :
![\begin{algorithm}[H]
\dontprintsemicolon
\Procedure{$insere(T, k)$}
{
$i \lo...
...{
$echanger(T[i - 1], T[i])$\;
$i \longleftarrow i - 1$
}
}
\end{algorithm}](img91.gif)
![]() un tableau
un tableau ![]() dont les
dont les
![]() premiers éléments sont triés, alors à la fin de son exécution,
les
premiers éléments sont triés, alors à la fin de son exécution,
les ![]() premiers éléments dont triés. Etant donné le programme suivant :
premiers éléments dont triés. Etant donné le programme suivant :
![\begin{algorithm}[H]
\dontprintsemicolon
\Procedure{$triInsertion(T[n])$}
{
\Pour{$i \in \{2, \ldots, n\}$}
{
$insere(T, i)$
}
}
\end{algorithm}](img95.gif)
![]() .
.
![]() forment une séquence de nombres
entiers strictement décroissante. Si l'on ne sort pas de la boucle
avec
forment une séquence de nombres
entiers strictement décroissante. Si l'on ne sort pas de la boucle
avec
![]() , on aura forcément
, on aura forcément ![]() après la dernière
itération. Prenons comme invariant de boucle la conjonction des
conditions suivantes :
après la dernière
itération. Prenons comme invariant de boucle la conjonction des
conditions suivantes :
![]() , alors la première tranche ne
contient aucun élément et la deuxième condition de l'invariant de
boucle permet de conclure que toute la tranche
, alors la première tranche ne
contient aucun élément et la deuxième condition de l'invariant de
boucle permet de conclure que toute la tranche
![]() est
triée. Si par contre, on sort de la boucle parce que
est
triée. Si par contre, on sort de la boucle parce que
![]() , alors comme, d'après l'invariant de boucle,
, alors comme, d'après l'invariant de boucle,
![]() et
et
![]() sont triées, alors
sont triées, alors
![]() est triée.
est triée.