



suivant: Un autre exemple
monter: Terminaison
précédent: Le principe
Table des matières
- Commençons par montrer que le programme s'arrête. La séquence formée
par les valeurs de
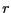 au fil des itérations est strictement
décroissante. Il y a donc nécessairement un moment où la valeur de
au fil des itérations est strictement
décroissante. Il y a donc nécessairement un moment où la valeur de
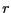 sera strictement inférieure à celle de
sera strictement inférieure à celle de 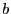 .
.
- Maintenant, nous pouvons terminer la preuve de validité :
- Si le programme s'arrête, c'est que la condition du Tant
que n'est plus satisfaite, donc que
 .
.
- Il reste à montrer que
 . Comme
. Comme 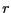 est diminué de
est diminué de 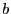 à
chaque itération, si
à
chaque itération, si  , alors à l'itération précédente la
valeur de
, alors à l'itération précédente la
valeur de 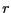 était
était
 , or
, or
 car
car  . Nous venons de montrer que si
. Nous venons de montrer que si 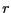 était strictement
négatif, alors la boucle se serait arrêtée à l'itération
précédente, ce qui est absurde. Donc nécessairement
était strictement
négatif, alors la boucle se serait arrêtée à l'itération
précédente, ce qui est absurde. Donc nécessairement  .
.
Résumons, le programme s'arrête avec  et la propriété
et la propriété  est vérifiée à chaque itération, ces deux propriétés nous
démontrent que l'algorithme effectue bien la division de
est vérifiée à chaque itération, ces deux propriétés nous
démontrent que l'algorithme effectue bien la division de 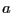 par
par 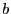 .
.




suivant: Un autre exemple
monter: Terminaison
précédent: Le principe
Table des matières
klaus
2010-08-05
 .
.
 . Comme
. Comme 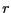 est diminué de
est diminué de 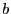 à
chaque itération, si
à
chaque itération, si  , alors à l'itération précédente la
valeur de
, alors à l'itération précédente la
valeur de 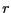 était
était
 , or
, or
 car
car  . Nous venons de montrer que si
. Nous venons de montrer que si 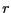 était strictement
négatif, alors la boucle se serait arrêtée à l'itération
précédente, ce qui est absurde. Donc nécessairement
était strictement
négatif, alors la boucle se serait arrêtée à l'itération
précédente, ce qui est absurde. Donc nécessairement  .
.