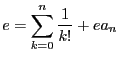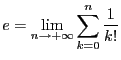suivant : 2.23.3 Changement de variable
remonter : 2.23.2 Intégration par parties
précédent : Exercice 5 - Relation
Pour tout
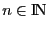 , on pose
, on pose
- Calculer
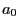
- Montrer que
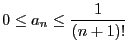
- En déduire que
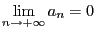
- Trouver une relation de récurrence entre
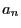 et
et 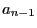
- En déduire que, pour tout
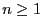 ,
,
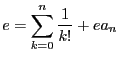
- Prouver que
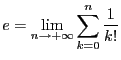
klaus
2011-02-14
![]() , on pose
, on pose