



suivant : 2. Exercices
remonter : 1.28.4 Estimations
précédent : 1.28.4.2 De R(x)
Si 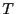 suit une loi exponentielle, la fonction de fiabilité est
entièrement déterminée par
suit une loi exponentielle, la fonction de fiabilité est
entièrement déterminée par
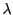 , plusieurs méthodes peuvent être utilisées pour l'estimer.
, plusieurs méthodes peuvent être utilisées pour l'estimer.
- On détermine en
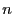 points du temps
points du temps
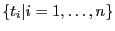 les
proportions
les
proportions
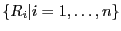 d'appareils tombés en panne
avant le moment
d'appareils tombés en panne
avant le moment 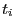 . Soit la série statistique à deux
variables
. Soit la série statistique à deux
variables
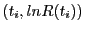 , on commence par déterminer le
coefficient de corrélation affine
, on commence par déterminer le
coefficient de corrélation affine 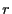 , si
, si 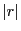 est suffisament
proche de
est suffisament
proche de 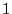 , alors on effectue une regression linéaire, sinon le
TBF ne suit probablement pas une loi exponentielle. On détermine
donc
, alors on effectue une regression linéaire, sinon le
TBF ne suit probablement pas une loi exponentielle. On détermine
donc 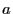 et
et 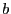 tels que
tels que
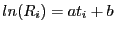 ,
autrement dit :
,
autrement dit :
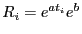 . Comme il va de soi que
. Comme il va de soi que 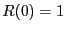 , alors
, alors 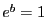 . D'où
. D'où
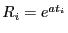 , on estime donc
, on estime donc 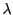 avec
avec 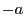 .
.
- On estime le MTBF sur un échantillon, comme
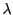 est son
inverse, il est trivial à estimer.
est son
inverse, il est trivial à estimer.
- On utilise le fait que
Il suffit alors de déterminer le point du temps 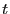 où une proportion
où une proportion
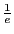 d'appareils sont opérationnels pour estimer
d'appareils sont opérationnels pour estimer
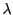 avec
avec 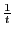 .
.




suivant : 2. Exercices
remonter : 1.28.4 Estimations
précédent : 1.28.4.2 De R(x)
klaus
2011-02-14
![]() suit une loi exponentielle, la fonction de fiabilité est
entièrement déterminée par
suit une loi exponentielle, la fonction de fiabilité est
entièrement déterminée par
![]() , plusieurs méthodes peuvent être utilisées pour l'estimer.
, plusieurs méthodes peuvent être utilisées pour l'estimer.