



suivant : 1.26 Estimations
remonter : 1.25.3 Résolution
précédent : 1.25.3.2 Equations différentielles linéaires
La méthode utilisée est dite variation de la constante,
derrière la dimension comique de cette terminologie se cache
une méthode assez astucieuse. Exposons la méthode de résolution d'une
équation différentielle linéaire homogène du premier ordre 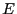 :
:
- Soit
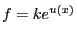 la solution générale de l'équation homogène associée.
la solution générale de l'équation homogène associée.
- On pose
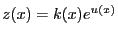 , en remplaçant
, en remplaçant 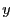 et
et 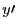 par
respectivement
par
respectivement 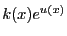 et
et
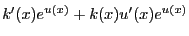 , on obtient une
expression de
, on obtient une
expression de 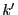 . Il ne reste plus qu'à la primitiver pour
trouver
. Il ne reste plus qu'à la primitiver pour
trouver 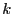 . On alors définit
. On alors définit 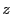 , qui est alors une solution particulière de
, qui est alors une solution particulière de 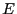 .
.
- La solution générale
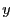 de
de 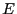 est de la forme
est de la forme
Illustrons cette méthode par la résolution de
- Résolvons l'équation homogène
on a 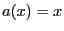 et
et 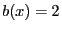 , comme
, comme
alors la solution générale de cette équation homogène est
- Posons
on a
Substituons 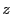 à
à 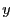 dans l'équation, on a alors
dans l'équation, on a alors
ce qui équivaut à
On déduit une expression de 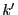 ,
,
D'où,
Posons
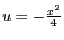 , alors
, alors
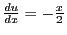 ssi
ssi 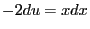 , donc
, donc
Et la fonction constante
est une solution particulière de l'équation
(c'est trivial à vérifier)
- La solution générale de l'équation
est donc
(c'est aussi trivial à vérifier)




suivant : 1.26 Estimations
remonter : 1.25.3 Résolution
précédent : 1.25.3.2 Equations différentielles linéaires
klaus
2011-02-14
![]() :
: