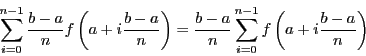![\includegraphics[width=12cm]{chapitres/integralesOption/rectangles.eps}](img1101.png)
|
La première méthode consiste à subdiviser l'aire que l'on souhaite
calculer en rectangles. Soit
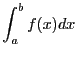 l'intégrale dont on
cherche à approcher la valeur. On subdivise l'intervalle
l'intégrale dont on
cherche à approcher la valeur. On subdivise l'intervalle ![]() en
en
![]() intervalles d'amplitude
intervalles d'amplitude
![]() . Nous
obtenons ainsi les
. Nous
obtenons ainsi les ![]() intervalles :
intervalles :
On remarque que ![]() est la borne supérieure du
dernier intervalle. Le
est la borne supérieure du
dernier intervalle. Le ![]() -ème intervalle est la base d'un
rectangle dont les quatre sommets ont pour coordonnées
-ème intervalle est la base d'un
rectangle dont les quatre sommets ont pour coordonnées
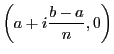
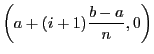
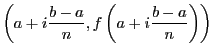
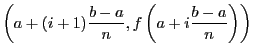
La surface d'un tel rectangle est donnée par
On approche
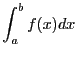 en additionnant les
aires des rectangles :
en additionnant les
aires des rectangles :