suivant : 1.21 Loi de Laplace-Gauss remonter : 1.20.2 Loi de Poisson précédent : 1.20.2.2 Définitions

1.20.2.3 Espérance mathématique et variance

Si $X$ suit $\mathcal{P}(\lambda)$ alors $E(X) = V(X) = \lambda$. On obtient ces résultats en calculant

$$E(X) = \lim_{n \longrightarrow + \infty} \sum_{i = 0}^n i\frac{\lambda^i e^{-\lambda}}{i!}= \ldots = \lambda$$

Et

$$V(X) = \lim_{n \longrightarrow + \infty} \sum_{i = 0}^n (i - \lambda)^2\frac{\lambda^i e^{-\lambda}}{i!}= \ldots = \lambda$$

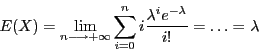
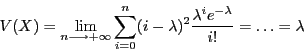
Les étapes intermédiaires sont très techniques et vous sont volontairement occultées, les élèves suivant le programme de maths option pourront revenir sur ces formules et tenter de les démontrer.