Soit ![]() une varible aléatoire suivant une loi de Poisson de paramètre
une varible aléatoire suivant une loi de Poisson de paramètre
![]() , ce que l'on note
, ce que l'on note ![]() suit
suit
![]() , alors
, alors
A chaque fois que vous aurez à utiliser la loi de Poisson, cela sera
précisé dans l'énoncé. Résolvons l'exemple : soit ![]() la variable
aléatoire "nombre de clients arrivés entre
la variable
aléatoire "nombre de clients arrivés entre ![]() heures et
heures et ![]() heures". Nous admettrons que
heures". Nous admettrons que ![]() suit
suit
![]() . Alors
. Alors
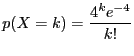 . Calculons
. Calculons
![]() à
à
![]() près.
près.