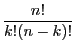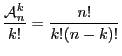 sous-ensembles à
sous-ensembles à 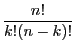
Nous tirons simultanément ![]() boules dans une urne contenant
boules dans une urne contenant ![]() boules. Combien de sous-ensembles à
boules. Combien de sous-ensembles à ![]() d'un ensemble à
d'un ensemble à ![]() éléments
pouvons-nous former de la sorte ? Ce problème revient à déterminer le
cardinal de
éléments
pouvons-nous former de la sorte ? Ce problème revient à déterminer le
cardinal de
![]() . Nous savons que le nombre de
. Nous savons que le nombre de ![]() -uplets qu'il est possible de
former avec
-uplets qu'il est possible de
former avec ![]() éléments est
éléments est
![]() . Or,
chaque élément de
. Or,
chaque élément de ![]() sera associé à plusieurs
sera associé à plusieurs ![]() -uplets. Nous savons
par ailleurs que le nombre de façon d'ordonner
-uplets. Nous savons
par ailleurs que le nombre de façon d'ordonner ![]() éléments est
éléments est
![]() . Il y a donc
. Il y a donc ![]() fois plus de
fois plus de ![]() -uplets formés avec
-uplets formés avec ![]() éléments que de sous-ensembles à
éléments que de sous-ensembles à ![]() éléments de
éléments de
![]() . Nous en déduisons qu'il y a
. Nous en déduisons qu'il y a
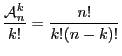 sous-ensembles à
sous-ensembles à ![]() éléments de
éléments de
![]() . Nous noterons
. Nous noterons
![]() le nombre
le nombre