Triangle de Pascal

Le triangle de Pascal est un tableau triangulaire de taille infinie dont les lignes sont indicées par $n$ et les colonnes par $p$, les indices commençant à $0$. Les seules case du trianles renseignées sont celles dont les indices vérifient $0 \leq p \leq n$. Les valeurs se trouvant à la ligne d'indice $n$ et la colonne d'indice $p$ du triangle de Pascal est $\mathcal{C}_n^p$, on a ainsi

$(n, p)$		$p =$	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$\ldots$
$n =$	$0$		$1$
	$1$		$1$	$1$
	$2$		$1$	$2$	$1$
	$3$		$1$	$3$	$3$	$1$
	$4$		$1$	$4$	$6$	$4$	$1$
	$5$		$1$	$5$	$10$	$10$	$5$	$1$
	$6$		$1$	$6$	$15$	$20$	$15$	$6$	$1$
	$\ldots$		$\ldots$	$\ldots$	$\ldots$	$\ldots$	$\ldots$	$\ldots$	$\ldots$	$\ldots$

Vous remarquez que la propriété $$\mathcal{C}_n^0 = 1$$ traduit le fait que la première colonne ne comporte que des $1$. Comme chaque ligne est symétrique alors $$\mathcal{C}_n^p = \mathcal{C}_n^{n-p}$$. Pour chaque ligne, le premier élément est $1$, donc la symétrie fait que le dernier est $1$ aussi. La propriété $$\mathcal{C}_n^p = \mathcal{C}_{n-1}^{p-1} + \mathcal{C}_{n-1}^{p}$$ traduit le fait que chaque élément $$\mathcal{C}_n^p$$ ne se trouvant pas dans la première colonne ou sur la diagonale est la somme de celui qui est au dessus $$\mathcal{C}_{n - 1}^p$$ et de celui qui est juste à gauche de ce dernier $$\mathcal{C}_{n - 1}^{p - 1}$$. Si on somme les éléments sur chaque ligne, on obtient des puissances successives de $2$ :

$(n, p)$		$p =$	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$\ldots$	$$\sum_{p = 0}^n \mathcal{C}_n^p$$
$n =$	$0$		$1$								$2^0$
	$1$		$1$	$1$							$2^1$
	$2$		$1$	$2$	$1$						$2^2$
	$3$		$1$	$3$	$3$	$1$					$2^3$
	$4$		$1$	$4$	$6$	$4$	$1$				$2^4$
	$5$		$1$	$5$	$10$	$10$	$5$	$1$			$2^5$
	$6$		$1$	$6$	$15$	$20$	$15$	$6$	$1$		$2^6$
	$\ldots$		$\ldots$	$\ldots$	$\ldots$	$\ldots$	$\ldots$	$\ldots$	$\ldots$	$\ldots$	...

Cette propriété se traduit 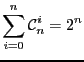$$\sum_{i=0}^{n}\mathcal{C}_n^i = 2^n$$. L'identité remarquable $(a + b)^n$ s'écrit à l'aide des coefficients su triangle de Pascal. Par exemple,

$$(a + b)^3 = a^3 + 3a^2b + 3 ab^2 + b^3$$

Vous remarquez que le développement de $(a + b)^3$ s'ecrit avec un polynome à deux variable dont la somme des exposants de chaque terme est $3$, chaque terme est donc de la forme $a^ib^{3 - i}$. Les coefficients devant chaque termes sont issus de la ligne d'indice $3$ du triangle de Pascal, à savoir $(1, 3, 3, 1)$, autrement dit $$(\mathcal{C}_3^0, \mathcal{C}_3^1, \mathcal{C}_3^2, \mathcal{C}_3^3)$$. Donc

$$(a + b)^3 = \sum_{i = 0}^3 \mathcal{C}_3^i a^ib^{n-i}$$

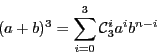
On a plus généralement que

$$(a + b)^n = \sum_{i=0}^{n}\mathcal{C}_n^ia^ib^{n-i}$$

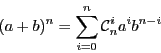
Par exemple,

$$(a + b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4$$

Le soin de le démontrer par récurrence vous est laissé.