Liens avec les ensembles

Le nombre de façons d'ordonner $n$ éléments distincts est donnée par $n!$ (la preuve vous est laissé en exercice).

Propriété B.4.2   Le nombre de sous-ensembles à $k$ éléments d'un ensemble $E$ à $n$ éléments, à savoir $\vert\{ x \vert (x \subset E) \wedge (\vert x\vert = k) \}\vert$ est donné par $\mathcal{C}_n^k$.

On le démontre par récurrence sur $n$,

• si $n = 0$, le seul ensemble à $0$ éléments est $\emptyset$, son seul sous-ensemble est $\emptyset$, donc
  
  $$\vert\{ x \vert (x \subset \emptyset) \wedge (\vert x\vert = 0) \}\vert = \vert\{ \emptyset \}\vert= 1 = \mathcal{C}_0^0$$
  
  

• Supposons que pour tout ensemble $E^\prime$ à $n - 1 \geq 0$ éléments, et tout $k^\prime \in \{0, \ldots, n-1\}$,
  
  $$\vert\{ x \vert (x \subset E^\prime) \wedge (\vert x\vert = k^\prime) \}\vert = \mathcal{C}_{n-1}^{k^\prime}$$
  
  
  Considérons un ensemble $E$ à $n \geq 1$ éléments et une valeur $k \in \{0, \ldots, n\}$, montrons que le cardinal de
  
  $$P = \{ x \vert (x \subset E) \wedge (\vert x\vert = k) \}$$
  
  
  est $\mathcal{C}_{n}^{k}$
  • Si $k \in \{1, \ldots, n-1\}$, choisissons un élément arbitraire $e \in E$, cet élément existe nécessairement car $\vert E\vert = n \geq 1$. On décompose $\{ x \vert (x \subset E) \wedge (\vert x\vert = k) \}$ en deux ensembles $P_1$ et $P_2$. $P_1$ est l'ensemble des sous-ensembles de $E$ à $k$ éléments qui contiennent $e$, défini par

    
    

    $$P_1 = \{ x \vert (x \subset E) \wedge (\vert x\vert = k) \wedge (e \in x) \}$$
    
    

    $P^\prime$ est celui des sous-ensembles à $k$ éléments qui ne contiennent pas $e$,

    
    

    $$P_2 = \{ x \vert (x \subset E) \wedge (\vert x\vert = k) \wedge (e \not \in x) \}$$
    
    

    On remarque que $P_1 \cup P_2 = P$ et que $P_1 \cap P_2 = \emptyset$, donc $\vert P\vert = \vert P_1\vert + \vert P_2\vert$. Comme $P_2$ est l'ensemble des sous-ensembles à $k$ éléments de $E-\{e\}$, on le redéfinit de la sorte :

    
    

    $$P_2 = \{ x \vert (x \subset E-\{e\}) \wedge (\vert x\vert = k) \}$$
    
    

    Comme $\vert E-\{e\}\vert = n-1$ et $k \in \{1, \ldots, n-1\}$, alors par hypothèse de récurrence, $\vert P_2\vert = \mathcal{C}_{n-1}^k$. Par ailleurs, chaque élement $x$ de $P_1$ se décompose de la sorte : $x = x^\prime \cup \{e\}$ où $x^\prime$ est un ensemble à $(k-1)$ éléments ne contenant pas $e$. Donc

    
    

    $$P_1 = \{ x^\prime \cup \{e\} \vert (x^\prime \subset E-\{e\}) \wedge (\vert x^\prime\vert = k-1)\}$$
    
    

    Il a donc autant d'élément dans $P_1$ que de sous-ensembles à $k-1$ éléments de $E-\{e\}$. Comme $\vert E-\{e\}\vert = n-1$ et $(k-1) \in \{0, \ldots, n-2\}$, alors par hypothèse de récurrence, on a $\vert P_1\vert = \mathcal{C}_{n-1}^{k-1}$. De ce fait $\vert P\vert = \mathcal{C}_{n-1}^k + \mathcal{C}_{n-1}^{k-1} = \mathcal{C}_{n}^{k}$.

  • Dans le cas où $k = 0$ et $n \geq 1$, on remarque que

    
    

    $$P = \{ x \vert (x \subset E) \wedge (\vert x\vert = 0) \} = \{ \emptyset \}$$
    
    

    et que par conséquent $\vert P\vert = \vert\{ \emptyset \}\vert = 1 = \mathcal{C}_{n}^{0}$

  • Il nous reste à traiter le cas où $k = n$ et $n \geq 1$, on remarque que

    
    

    $$P = \{ x \vert (x \subset E) \wedge (\vert x\vert = \vert E\vert) \} = \{ E \}$$
    
    

    et que par conséquent $\vert P\vert = \vert\{ E \}\vert = 1 = \mathcal{C}_{n}^{n}$.

  On a bien

  
  

  $$\{ x \vert (x \subset E) \wedge (\vert x\vert = k) \} = \mathcal{C}_{n}^{k}$$
  
  

  Pour tout $k \in \{0, \ldots, n\}$.

Etant donné un ensemble $E$ à $n$ éléments, dénombrons les parties de $E$, ce qui revient à calculer $\vert\mathcal{P}(E)\vert$. Pour ce faire, on décompose $\mathcal{P}(E)$ en $n+1$ sous-ensembles $\mathcal{P}_k(E)$, $k \in \{0, \ldots, n\}$, définis comme suit

$$\mathcal{P}_k(E) = \{e \vert (e \subset E) \wedge (\vert e\vert = k)\}$$

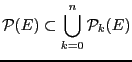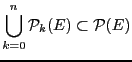On remarque que pour tout $e \subset E$, $e \in \mathcal{P}_{\vert e\vert}(E)$, donc $$\mathcal{P}(E) \subset \bigcup_{k=0}^n \mathcal{P}_k(E)$$. Réciproquement, pour tout $k \in \{0, \ldots, n\}$, tout élément de $\mathcal{P}_k(E)$ est, par définition, une partie de $E$, donc $$\bigcup_{k=0}^n \mathcal{P}_k(E) \subset \mathcal{P}(E)$$. On déduit de cette double inclusion que

$$\mathcal{P}(E) = \bigcup_{k=0}^n \mathcal{P}_k(E)$$

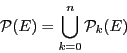
Deux ensembles $\mathcal{P}_k(E)$ et $\mathcal{P}_{k^\prime}(E)$ tels que $k \not = k^\prime$ sont nécessairements disjoints(si ça vous semble pas évident, cherchez un contre-exemple et vous comprendrez pourquoi...). Donc

$$\vert \bigcup_{k=0}^n \mathcal{P}_k(E) \vert = \sum_{k=0}^n \vert\mathcal{P}_k(E)\vert$$

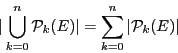
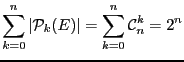Si cette propriété ne vous parle pas, démontrez-la par récurrence en utilisant le fait que si $A \cap B = \emptyset$, alors $\vert A \cap B\vert = \vert A\vert + \vert B\vert$. Nous avons démontré que $$\forall k \in \{0, \ldots, n\}, \vert\mathcal{P}_k(E) \vert = \mathcal{C}_{n}^{k}$$. Donc $$\sum_{k=0}^n \vert\mathcal{P}_k(E)\vert = \sum_{k=0}^n \mathcal{C}_{n}^{k} = 2^n$$. Le nombre de parties d'un ensemble à $n$ éléments est donc $2^n$. Il vous est possible, de vérifier ce résultat par récurrence, le raisonnement est analogue à celui employé pour prouver que $\vert\{ x \vert (x \subset E) \wedge (\vert x\vert = k) \}\vert = \mathcal{C}_{n}^{k}$, mais en plus facile.