



suivant: Exercice 1
monter: Arithmétique modulaire
précédent: Arithmétique modulaire
Table des matières
Définition 15.1.1
si
On dit alors que 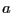 est congru à
est congru à 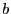 modulo
modulo  .
.
Autrement dit, 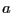 est
est 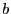 congru à
congru à 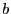 modulo
modulo  si et seulement si
si et seulement si
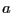 et
et 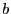 ont le même reste de la division par
ont le même reste de la division par  . Plus
formellement,
. Plus
formellement,
Propriété 15.1.1
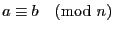 si et seulement si
si et seulement si
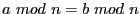 .
.
En effet, si 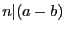 , alors il existe
, alors il existe  tel que
tel que 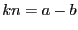 . Divisons
. Divisons 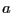 et
et 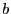 par
par  , il existe
, il existe 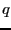 ,
, 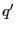 ,
, 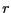 et
et
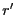 tels que
tels que 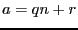 et
et
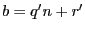 , avec
, avec
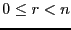 et
et
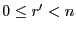 . Donc
. Donc 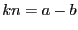 équivaut à
équivaut à
ssi
ssi
Donc
Or,
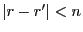 , donc
, donc  ne peut diviser
ne peut diviser
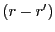 que si
que si
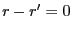 . On a donc
. On a donc 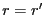 , comme
, comme
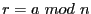 et
et
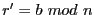 , alors
, alors
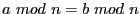 .
.
Réciproquement, supposons
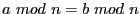 . Divisons
. Divisons 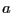 et
et 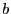 par
par  , il existe
, il existe 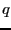 ,
, 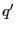 et
et 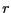 tels que
tels que 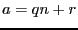 et
et
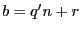 , avec
, avec 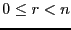 . Donc
. Donc
ssi
ssi
Donc, 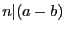 .
.
Sous-sections




suivant: Exercice 1
monter: Arithmétique modulaire
précédent: Arithmétique modulaire
Table des matières
klaus
2010-08-05
![]() est
est ![]() congru à
congru à ![]() modulo
modulo ![]() si et seulement si
si et seulement si
![]() et
et ![]() ont le même reste de la division par
ont le même reste de la division par ![]() . Plus
formellement,
. Plus
formellement,
![]() , alors il existe
, alors il existe ![]() tel que
tel que ![]() . Divisons
. Divisons ![]() et
et ![]() par
par ![]() , il existe
, il existe ![]() ,
, ![]() ,
, ![]() et
et
![]() tels que
tels que ![]() et
et
![]() , avec
, avec
![]() et
et
![]() . Donc
. Donc ![]() équivaut à
équivaut à