



suivant: Rotations
monter: Complexité dans le pire
précédent: Complexité dans le pire
Table des matières
Soit un ensemble
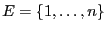 de
de  clés. Nous voulons
déterminer le nombre moyen
clés. Nous voulons
déterminer le nombre moyen 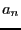 de noeuds visités lors de la
recherche d'une de ces clés dans un ABR contenant les clés de
de noeuds visités lors de la
recherche d'une de ces clés dans un ABR contenant les clés de 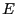 . On
suppose que les ordres d'insertion sont équiprobables. Par ailleurs,
on considère que la probabilité de rechercher la clé
. On
suppose que les ordres d'insertion sont équiprobables. Par ailleurs,
on considère que la probabilité de rechercher la clé 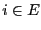 est
est
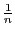 .
.
- Montrer que la probabilité que la racine ait la clé
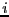 est
est
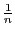 .
.
- Notons
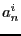 le nombre moyen de comparaisons nécessaires
pour trouver une clé dans un arbre à
le nombre moyen de comparaisons nécessaires
pour trouver une clé dans un arbre à  clés dont la racine
porte la clé
clés dont la racine
porte la clé 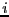 . Exprimer
. Exprimer 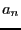 en fonction de
en fonction de
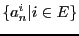 .
.
- On pose
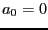 . Combien valent
. Combien valent 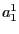 et
et 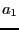 ?
?
- Montrer que
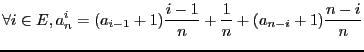
- En déduire que
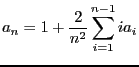
- En déduire que
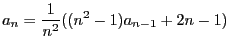
- Utiliser le fait que
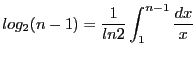 et que
et que
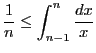 pour prouver par récurrence qu'il existe
pour prouver par récurrence qu'il existe 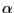 tel que
tel que
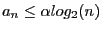
- Quelle est la complexité moyenne de la recherche d'une clé de
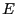 dans un ABR ?
dans un ABR ?




suivant: Rotations
monter: Complexité dans le pire
précédent: Complexité dans le pire
Table des matières
klaus
2010-08-05
![]() de
de ![]() clés. Nous voulons
déterminer le nombre moyen
clés. Nous voulons
déterminer le nombre moyen ![]() de noeuds visités lors de la
recherche d'une de ces clés dans un ABR contenant les clés de
de noeuds visités lors de la
recherche d'une de ces clés dans un ABR contenant les clés de ![]() . On
suppose que les ordres d'insertion sont équiprobables. Par ailleurs,
on considère que la probabilité de rechercher la clé
. On
suppose que les ordres d'insertion sont équiprobables. Par ailleurs,
on considère que la probabilité de rechercher la clé ![]() est
est
![]() .
.
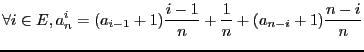
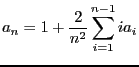
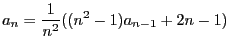
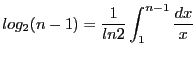 et que
et que
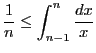 pour prouver par récurrence qu'il existe
pour prouver par récurrence qu'il existe