L'identité remarquable ![]() s'écrit à l'aide des coefficients su triangle de Pascal. Par
exemple,
s'écrit à l'aide des coefficients su triangle de Pascal. Par
exemple,
Vous remarquez que le développement de ![]() s'ecrit avec un
polynome à deux variables dont la somme des exposants de chaque terme
est
s'ecrit avec un
polynome à deux variables dont la somme des exposants de chaque terme
est ![]() , chaque terme est donc de la forme
, chaque terme est donc de la forme ![]() . Les
coefficients devant chaque terme sont issus de la ligne d'indice
. Les
coefficients devant chaque terme sont issus de la ligne d'indice ![]() du triangle de Pascal, à savoir
du triangle de Pascal, à savoir ![]() , autrement dit
, autrement dit
![]() . Donc
. Donc
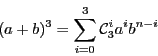
On généralise cette formule avec la propriété suivante, appelée Binôme de Newton.
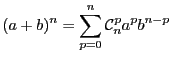
Par exemple,
On remarque par ailleurs que la formule
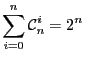 correspond au cas particulier du
binôme de Newton où
correspond au cas particulier du
binôme de Newton où ![]() .
.