Si on somme les éléments sur chaque ligne, on obtient des puissances
successives de ![]() :
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
| |
|
|
|
||||||||
| |
|
|
|
|
|||||||
| |
|
|
|
|
|
||||||
| |
|
|
|
|
|
|
|||||
| |
|
|
|
|
|
|
|
||||
| |
|
|
|
|
|
|
|
|
|||
| |
|
|
|
|
|
|
|
|
... |
On a donc
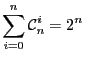 .
.