



suivant : Exercice 8
remonter : 4.1.5 Parties
précédent : 4.1.5.1 Inclusion
Définition 4.1.10
L'ensemble
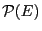 des parties de
des parties de 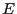 , est défini par
, est défini par
 est donc l'ensemble de tous les ensembles inclus dans
est donc l'ensemble de tous les ensembles inclus dans
 . Par exemple,
. Par exemple,
On remarque
que
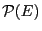 est un ensemble d'ensembles. Prennez note du fait
que
est un ensemble d'ensembles. Prennez note du fait
que 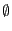 est un sous-ensemble de tous les ensembles, y compris
de lui-même, et que le seul ensemble contenu dans
est un sous-ensemble de tous les ensembles, y compris
de lui-même, et que le seul ensemble contenu dans 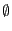 est
est
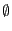 . A votre avis, que vaut
. A votre avis, que vaut
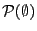 ? Cette
question vous amènera à distinuer
? Cette
question vous amènera à distinuer 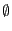 de
de 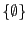 , qui
est l'ensemble qui contient l'ensemble vide.
, qui
est l'ensemble qui contient l'ensemble vide.
Alexandre
2009-05-26
![]() est donc l'ensemble de tous les ensembles inclus dans
est donc l'ensemble de tous les ensembles inclus dans
![]() . Par exemple,
. Par exemple,