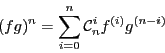suivant : Exercice 4 - Dérivée
remonter : 3.2 Exemple
précédent : Exercice 2 - Dérivée
On note 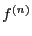 la dérivée
la dérivée  -ième de
-ième de  . Prouvez par récurrence
la formule de Leibniz :
. Prouvez par récurrence
la formule de Leibniz :
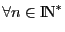
Alexandre
2009-05-26
![]() la dérivée
la dérivée ![]() -ième de
-ième de ![]() . Prouvez par récurrence
la formule de Leibniz :
. Prouvez par récurrence
la formule de Leibniz :
![]()