suivant : Exercice 5 - Autres
remonter : 2.2 Propriétés
précédent : Exercice 3 - Calculs
- Développer
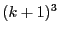
- En déduire de
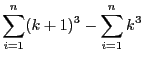 une expression de
une expression de
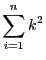 en fonction de
en fonction de
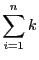 et de
et de
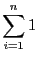
- Donner une expression sans
 de
de
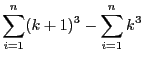
- Déduire des deux questions
précédentes une expression
sans
 de
de
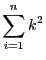
- En adoptant une démarche
similaire, donner une
expression sans
 de
de
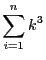
Alexandre
2009-05-26
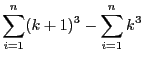 une expression de
une expression de
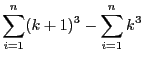
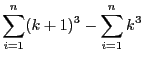 une expression de
une expression de