



suivant : 2.13 Exponentielles
remonter : 2.12 Logarithmes
précédent : Exercice 8 - Théorème
Rappelons que si  est une fonction définie sur un ensemble
est une fonction définie sur un ensemble  ,
alors la valeur de
,
alors la valeur de  , si elle existe, est donnée par
, si elle existe, est donnée par
- Prouvez que
avec  une
fonction dérivable,
une
fonction dérivable, 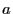 et
et 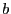 deux réels
deux réels
- Prouvez que
où  et
et
 sont deux fonctions dérivables
sont deux fonctions dérivables
- Prouvez que
où 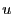 est une fonction
dérivable sur toutes les valeurs où elle ne s'annule pas
est une fonction
dérivable sur toutes les valeurs où elle ne s'annule pas
- Prouvez que
où  et
et
 sont deux fonctions dérivables
sont deux fonctions dérivables
- Prouvez que
où  et
et
 sont deux fonctions dérivables sur les valeurs où
sont deux fonctions dérivables sur les valeurs où  ne
s'annule pas
ne
s'annule pas
klaus
2011-02-14
![]() est une fonction définie sur un ensemble
est une fonction définie sur un ensemble ![]() ,
alors la valeur de
,
alors la valeur de ![]() , si elle existe, est donnée par
, si elle existe, est donnée par