suivant : 1.4.2.4 Deux pièges remonter : 1.4.2 Equations du premier précédent : 1.4.2.2 Techniques de résolution

1.4.2.3 Deux cas particuliers

Considérons l'équation $2x = x + x$, il va de soi que tout réel est solution. Tentons de la résoudre :

$$\begin{array}{l l l l} &2x& = & x + x \\ \iff & 2x - x - x & = & 0\\ \iff & 0x & = & 0\\ \iff & 0 & = & 0\\ \end{array}$$

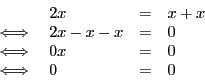
Le raisonnement par équivalences successives nous montre que $2x = x + x$ et $0 = 0$ sont deux équations équivalentes. Cela signifie que la valeur de vérité de la relation $2x = x + x$ ne dépend pas de $x$, et qu'elle équivaut à $0 = 0$, comme $0 = 0$ est vrai, on en déduit que $2x = x + x$ équivaut à vrai, donc que tout réel est solution de $2x = x + x$. On rédigera donc de la sorte :

$$\begin{array}{l l l l} &2x& = & x + x \\ \iff & 2x - x - x ... ...0x & = & 0\\ \iff & 0 & = & 0\\ \iff & x \in R\\ \end{array}$$

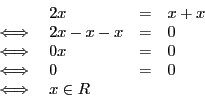
De même, considérons l'équation

$$\begin{array}{l l l l} &x& = & x + 1 \\ \iff & x - x & = & 1\\ \iff & 0x & = & 1\\ \iff & 0 & = & 1\\ \end{array}$$

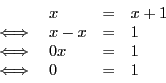
Cette fois-ci, le raisonnement par équivalences successives nous montre que l'équation $x = x + 1$ équivaut à une relation qui est toujours fausse, cela signifie que vous pouvez substituer n'importe quelle valeur à $x$, vous ne trouverez aucun réel que vérifiera la relation. On écrira donc

$$\begin{array}{l l l l} &x& = & x + 1 \\ \iff & x - x & = & ... ... 1\\ \iff & 0 & = & 1\\ \iff & x \in \emptyset\\ \end{array}$$

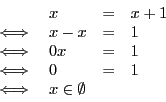
On précisera dans ce type de cas que l'équation n'a pas de solution.

suivant : 1.4.2.4 Deux pièges remonter : 1.4.2 Equations du premier précédent : 1.4.2.2 Techniques de résolution