![\includegraphics[width=12cm]{chapitres/integralesOption/trapezes.eps}](img1111.png)
|
La méthode des trapèzes est une amélioration de la méthode des
rectangles. Pour chaque subdivision
![$\displaystyle \left[a + i\frac{b
- a}{n}, a + (i+1)\frac{b - a}{n}\right]$](img1112.png) , on approche l'aire
située sous la courbe par un trapèze dont les sommets ont les
coordonnées suivantes :
, on approche l'aire
située sous la courbe par un trapèze dont les sommets ont les
coordonnées suivantes :
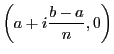
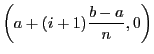
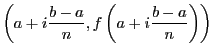
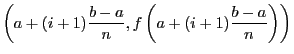
Vous remarquez que seul le point en haut à droite diffère de la méthode précédente. On calcule la surface d'un trapèze avec la formule suivante :
Où ![]() est la hauteur du trapèze,
est la hauteur du trapèze, ![]() la longueur de la petite base et
la longueur de la petite base et
![]() la longueur de la grande base. La hauteur du
la longueur de la grande base. La hauteur du ![]() -ème trapèze est
donnée par
-ème trapèze est
donnée par
![]() , les deux bases ont pour
longueurs
, les deux bases ont pour
longueurs
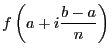 et
et
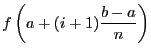 . La surface du
. La surface du
![]() -ème trapèze est donc donnée par
-ème trapèze est donc donnée par
On approche
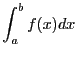 en additionnant les
aires des trapèzes :
en additionnant les
aires des trapèzes :
![\begin{displaymath}
\sum_{i = 0}^{n-1} \left(\frac{b - a}{2n}\right)\left[f\lef...
... a}{n}\right) + f\left(a + (i+1)\frac{b - a}{n}\right)\right]
\end{displaymath}](img1119.png)
Plaçons
![]() en facteur,
en facteur,
![\begin{displaymath}
\frac{b - a}{2n}\sum_{i = 0}^n \left[f\left(a + i\frac{b -
a}{n}\right) + f\left(a + (i+1)\frac{b - a}{n}\right)\right]
\end{displaymath}](img1121.png)
On remarque que
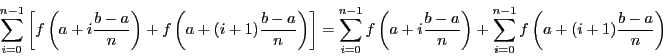
En réindiçant la deuxième somme, on a
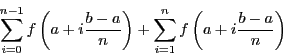
En sortant le premier terme de la première somme et le dernier terme de la deuxième somme, on a
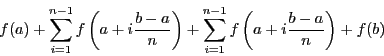
On remarque que les deux sommes sont les mêmes, on a donc
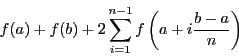
On approche donc
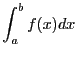 avec
avec
![\begin{displaymath}
\frac{b - a}{2n}\left[f(a) + f(b) +
2\sum_{i = 1}^{n-1} f\left(a + i\frac{b -
a}{n}\right)\right]
\end{displaymath}](img1126.png)