



suivant : 1.2.4 Parties
remonter : 1.2 Ensembles
précédent : 1.2.2 Intervalles
Définition 1.2.4
L'union de deux ensembles 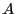 et
et 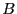 , notée
, notée 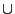 , est
définie par
, est
définie par
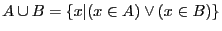 .
.
Un élément appartient à 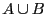 s'il
appartient à
s'il
appartient à 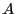 , ou s'il appartient à
, ou s'il appartient à 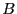 . Par exemple,
. Par exemple,
Définition 1.2.5
L'intersection de deux ensembles 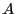 et
et 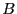 , notée
, notée 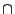 ,
est définie par
,
est définie par
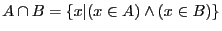 .
.
Un élément appartient à 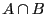 s'il
appartient à
s'il
appartient à 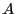 , et s'il appartient à
, et s'il appartient à 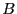 . Par exemple,
. Par exemple,
Définition 1.2.6
La différence de deux ensembles 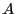 et
et 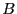 , notée
, notée
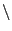 , est définie par
, est définie par
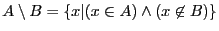 .
.
Un élément appartient à
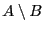 s'il appartient à
s'il appartient à 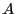 , mais pas à
, mais pas à 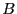 . Par
exemple,
. Par
exemple,
klaus
2011-02-14
![]() s'il
appartient à
s'il
appartient à ![]() , ou s'il appartient à
, ou s'il appartient à ![]() . Par exemple,
. Par exemple,
![]() s'il
appartient à
s'il
appartient à ![]() , et s'il appartient à
, et s'il appartient à ![]() . Par exemple,
. Par exemple,
![]() s'il appartient à
s'il appartient à ![]() , mais pas à
, mais pas à ![]() . Par
exemple,
. Par
exemple,