S'il y a ![]() boules numérotées de
boules numérotées de ![]() à
à ![]() dans cette urne et que
l'on tire successivement les
dans cette urne et que
l'on tire successivement les ![]() boules sans remise, nous voulons savoir
combien de
boules sans remise, nous voulons savoir
combien de ![]() -uplets il est possible de former avec
-uplets il est possible de former avec ![]() nombres
sélectionnés parmi
nombres
sélectionnés parmi ![]() sans que le même nombre apparaîsse deux
fois. Il y a au premier tirage
sans que le même nombre apparaîsse deux
fois. Il y a au premier tirage ![]() possibilités. Comme on ne peut pas
sélectionner la même valeur une deuxième fois, il y a au deuxième
tirage
possibilités. Comme on ne peut pas
sélectionner la même valeur une deuxième fois, il y a au deuxième
tirage ![]() possibilités. Au dernier tirage, il n'y a plus qu'
possibilités. Au dernier tirage, il n'y a plus qu'![]() possibilité. Le nombre de possibilités est donc
possibilité. Le nombre de possibilités est donc
![]() (factorielle
(factorielle ![]() ). Cela revient à
calculer le cardinal de l'ensemble
). Cela revient à
calculer le cardinal de l'ensemble
![]() est l'ensemble des
est l'ensemble des ![]() -uplets d'éléments distinct pris dans
-uplets d'éléments distinct pris dans
![]() . On note
. On note ![]() le cardinal de
le cardinal de ![]() . On remarque que
. On remarque que
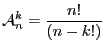 et que
et que
![]() . Ce cas est donc un cas
particulier du précédent. On reformuler ce résultat en concluant que
le nombre de façon d'ordonner
. Ce cas est donc un cas
particulier du précédent. On reformuler ce résultat en concluant que
le nombre de façon d'ordonner ![]() éléments est
éléments est ![]() .
.