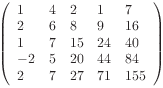
Écrire une procédure calculant la somme de deux matrices.
Écrire une procédure calculant la matrice transposée d’une matrice A de dimensions (n × p) de deux façons :
Écrire une procédure échangeant deux lignes d’une matrice.
Écrire une procédure calculant le produit de deux matrices.
Écrire une calculant l’indice de la colonne dont la somme des valeurs est la plus élevée.
Un triangle de Pascal peut être placé dans une matrice, dont seule la partie triangulaire inférieure est renseignée. La première ligne et la première colonne d’une triangle de Pascal ne contiennent que des 1. Et, si on note P(i, j) la valeur se trouvant dans la i-ème ligne et la j-ème colonne de cette matrice, alors on a
| m(i, j) = m(i−1, j−1) + m(i−1, j) |
pour tous i et j supérieurs ou égaux à 1. Écrire une procédure initialisant un triangle de Pascal à n lignes.
Écrire une procédure remplissant une matrice m de la façon suivante :
| m(i, j) = ij−1 |
Vous utiliserez le fait que
| ij = P(0, j)(i−1)0 + P(1, j)(i−1)1 + … + P(k, j)(i−1)k + … + P(j, j)(i−1)j |
où P(a, b) est l’élément se trouvant dans la ligne b+1 et la colonne a+1 du triangle de Pascal calculé dans l’exercice précédent.
Soit M une matrice à n lignes et à p colonnes, on note m(i, j) l’élément de M de trouvant à la i-ème ligne et à la j-ème colonne. M est une matrice de Toepliz si pour tout i ∈ {2, …, n} et pour tout j ∈ {2, …, p},
| m(i, j) = m(i−1, j) + m(i, j−1) |
Par exemple :
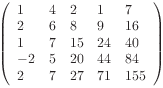
Écrire la procédure toepliz(entier : T[m, n] e/s) prenant en paramètre une matrice dont la première ligne et la première colonne sont initialisées. Cette procédure initialise tous les autres éléments de la matrice de sorte que T soit une matrice de Toepliz.
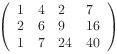 en
en
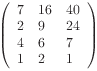 Écrire la procédure rotation(entier : T[m, n], Q[n, m]
e/s) affectant à la matrice Q le résultat de la rotation
de la matrice T.
Écrire la procédure rotation(entier : T[m, n], Q[n, m]
e/s) affectant à la matrice Q le résultat de la rotation
de la matrice T.