
Considérons un algorithme dont l’exécution donnerait :
Saisissez 10 valeurs : 4 90 5 -2 0 6 8 1 -7 39 Saisissez une valeur : -7 -7 est la 9-ième valeur saisie.
Comment rédiger un tel algorithme sans utiliser dix variables pour stocker les 10 valeurs ?
Une tableau est un regroupement de variables de même type, il est
identifié par un nom.
Chacune des variables du tableau est numérotée,
ce numéro s’appelle un indice. Chaque variable du tableau est
donc caractérisée par le nom du tableau et son indice.
Si par exemple, T est un tableau de 10 variables, alors chacune
d’elles sera numérotée et il sera possible de la retrouver en
utilisant simultanément le nom du tableau et l’indice de la
variable. Les différentes variables de T porteront des numéros de
1 à 10, et nous appellerons chacune de ces variables un
élément de T.
Une variable n’étant pas un tableau est appelée variable
scalaire, un tableau par opposition à une variable scalaire
est une variable non scalaire.
Comme les variables d’un tableau doivent être de même type, il convient de préciser ce type au moment de la déclaration du tableau. De même, on précise lors de la déclaration du tableau le nombre de variables qu’il contient. La syntaxe est :

Par exemple,

déclare un tableau T contenant 4 variables de type entier.
Les éléments d’un tableau à n éléments sont indicés de 1 à n. On note T[i] l’élément d’indice i du tableau T. Les quatre éléments du tableau de l’exemple ci-avant sont donc notés T[1], T[2], T[3] et T[4].
Nous pouvons maintenant rédiger l’algorithme dont le comportement est décrit au début du cours. Il est nécessaire de stocker 10 valeurs de type entier, nous allons donc déclarer un tableau E de la sorte :

La déclaration ci-dessus est celle d’un tableau de 10 éléments de type entier appelé E. Il convient ensuite d’effectuer les saisies des 10 valeurs. On peut par exemple procéder de la sorte :

La redondance des instructions de saisie de cet extrait sont d’une laideur rédhibitoire. Nous procéderons plus élégamment en faisant une boucle :

Ce type de boucle s’appelle un parcours de tableau. En règle générale on utilise des boucles pour manier les tableaux, celles-ci permettent d’effectuer un traitement sur chaque élément d’un tableau. Ensuite, il faut saisir une valeur à rechercher dans le tableau :

Nous allons maintenant rechercher la valeur t dans le tableau E. Considérons pour ce faire la boucle suivante :

Cette boucle parcourt le tableau jusqu’à trouver un élément de E qui ait la même valeur que t. Le problème qui pourrait se poser est que si t ne se trouve pas dans le tableau E, alors la boucle pourrait ne pas s’arrêter. Si i prend des valeurs strictement plus grandes que 10, alors il se produira ce que l’on appelle un débordement d’indice. Vous devez toujours veiller à ce qu’il ne se produise pas de débordement d’indice ! Nous allons donc faire en sorte que la boucle s’arrête si i prend des valeurs strictement supérieures à 10.

Il existe donc deux façons de sortir de la boucle :
On identifie donc la façon dont on est sorti de la boucle en testant la valeur de i :
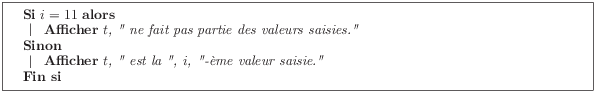
Si (i = 11), alors nous sommes sorti de la boucle parce que l’élément saisi par l’utilisateur ne trouve pas dans le tableau. Dans le cas contraire, t est la i-ème valeur saisie par l’utilisateur. Récapitulons :
