
Considérons la suite d’instructions suivante :
Vous l’aurez deviné, il s’agit des grandes lignes de la recette permettant de préparer des pâtes (si vous les voulez al dente, attendez un petit peu moins de 10 minutes). Cette recette ne vous expose pas le détail des réactions chimiques qui font que les pâtes cuisent en dix minutes, ni pourquoi il faut les égoutter. Il s’agit seulement d’une suite d’instructions devant être exécutées à la lettre. Si vous ne les suivez pas, vous prenez le risque que le résultat ne soit pas celui que vous attendez. Si vous décidez de suivre une recette, vous décidez de vous conformer aux instructions sans poser de questions. Par opposition, vous pouvez décider de créer vous-même une recette, cela vous demandera davantage de réflexion, et vous serez amené à élaborer d’une suite d’instructions qui vous permettra de retrouver le même résultat.
Considérons comme autre exemple une notice de montage. Elle est composée d’un ensemble d’étapes à respecter scrupuleusement. Il ne vous est pas demandé de vous interroger sur la validité de ces instructions, on vous demande juste de les suivre. Si vous vous conformez aux indications de la notice, vous parviendrez à monter votre bibliothèque Louis XVI. Si vous ne suivez pas la notice de montage, il vous restera probablement à la fin une pièce entre les mains, et vous aurez beau chercher où la placer, aucun endroit ne conviendra. Vous aurez alors deux solutions : soit vous démontez tout pour reprendre le montage depuis le début, soit vous placez cette pièce dans l’assiette qui est dans l’entrée en attendant le prochain déménagement, et en sachant que la prochaine fois, vous suivrez la notice... Cet exemple est analogue au premier, vous avez entre vos mains une suite d’instructions à exécuter, si vous les suivez, vous obtenez le résultat attendu, sinon, il y a de très fortes chances que n’obteniez pas le résultat escompté. De la même façon, le but n’est pas que vous vous demandiez pourquoi ou comment ça marche, la notice est faite pour que vous n’ayez pas à vous poser ce type de question. Si jamais vous décidez de créer un meuble (par exemple, une bibliothèque Nicolas Premier) à monter soi-même, il vous faudra fournir avec une notice de montage. C’est-à-dire une succession d’étapes que l’acquéreur de ce meuble devra suivre à la lettre.
On conclut de de la façon suivante : nous avons vu qu’il existait des séquences d’instructions faites pour être exécutée à la lettre et sans se poser de questions, c’est le principe de l’algorithme. Nous retiendrons donc que Un algorithme est une séquence d’instructions exécutée de façon logique mais non intelligente.
Les premiers algorithmes remontent à l’antiquité. Par exemple
l’algorithme de calcul du plus grand commun diviseur de deux nombres,
appelé maintenant "algorithme d’Euclide". Il s’agissait en général de
méthodes de calcul semblables à celle que vous utilisez depuis le
cours élémentaire pour additionner deux nombres à plusieurs
chiffres. Notez qu’à l’époque, on vous demandait juste d’appliquer la
méthode sans vous tromper, on ne vous a pas expliqué pourquoi cette
méthode marchait à tous les coups. Le principe était donc le même,
vous n’aviez pas le niveau en mathématiques pour comprendre pourquoi
la succession d’étapes qu’on vous donnait était valide, mais vous
étiez capable d’exécuter chaque étape de la méthode. Avant même
d’avoir dix ans, vous connaissiez donc déjà des algorithmes.
Le mot algorithme prend étymologiquement ses racines dans le nom d’un
mathématicien arabe du moyen âge : Al-Kawarizmi. Les algorithmes sont
extrêmement puissants : en concevant un algorithme, vous pouvez
décomposer un calcul compliqué en une succession d’étapes
compréhensibles, c’est de cette façon qu’on vous a fait faire des
divisions (opération compliquée) en cours moyen, à un âge où votre
niveau en mathématiques ne vous permettait pas de comprendre le
fonctionnement d’une division.
Contrairement aux mythe Matrix-Terminator-L’Odyssée de l’espace-I,
Robot-R2D2 (et j’en passe) un ordinateur fonctionne de la même façon
qu’un monteur de bibliothèque (rien à voir avec l’alpinisme) ou votre
cuisinier célibataire (il y a quand même des exceptions), il est
idiot et pour chaque chose que vous lui demanderez, il faudra lui dire
comment faire. Vous aller donc lui donner des successions
d’instructions à suivre, et lui les respectera à la lettre et sans
jamais se tromper. Une suite d’instructions de la sorte est fournie à
l’ordinateur sous la forme de programme. Pour coder un
programme, on utilise un langage de programmation, par
exemple C, Java, Pascal, VB... Selon le langage utilisé, une même
instruction se code différemment, nous ferons donc dans ce cours
abstraction du langage utilisé. Nous nous intéresserons uniquement à
la façon de combiner des instructions pour former des programmes,
indépendamment des langages de programmation. Le but de ce cours est
donc de vous apprendre à créer des algorithmes, c’est-à-dire à
décomposer des calculs compliqués en successions d’étapes simples.
Un algorithme se présente comme une liste d’instructions, elles sont écrites les unes au dessus des autres et elles sont exécutées dans l’ordre, lorsque l’on conçoit une algorithme, il faut toujours avoir en tête le fait que l’ordre des instructions est très important. Le premier concept nécessaire pour concevoir un algorithme est celui de variable.
Une variable est un emplacement de la mémoire dans lequel est stockée une valeur.
Une valeur est
Une variable a un type, qui détermine les valeurs que l’on pourra y placer.
Si une variable est de type numérique, il n’est possible d’y mettre que des valeurs numériques, si une variable est de type alphanumérique, il n’est possible d’y stocker que des valeurs alphanumériques.
L’affectation est une opération permettant de modifier la valeur d’une variable :

<nomvariable> est le nom de la variable dont on souhaite modifier la valeur, <valeur> est la valeur que l’on veut placer dans la variable. Notez bien que cette valeur doit être de même type que la variable. Par exemple,

place la valeur 5 dans la variable A. Si A contenait préalablement une valeur, celle-ci est écrasée. Il est possible d’affecter à une variable le résultat d’une opération arithmétique.

On peut aussi affecter à une variable la valeur d’une autre variable

La première instruction lit la valeur de B et la recopie dans A. la deuxième instruction, donc exécutée après la première, lit la valeur de B, lui additionne 2, et recopie le résultat dans A. Le fait que l’on affecte à A la valeur de B ne signifie pas que ces deux variables auront dorénavant la même valeur. Cela signifie que la valeur contenue dans B est écrasée par la valeur que contient A au moment de l’affectation. Si la par la suite, la valeur de A est modifiée, alors la valeur de B restera inchangée. Il est possible de faire figurer une variable simultanément à gauche et à droite d’une affectation :

Cette instruction augmente de 1 la valeur contenue dans A, cela s’appelle une incrémentation.
Quelles sont les valeurs des variables après l’exécution des instructions suivantes ?

Construisons un tableau nous montrant les valeurs des variables au fil des affectations :
| instruction | A | B | C | D |
| début | n.i | n.i | n.i | n.i |
| A ←— 1 | 1 | n.i | n.i | n.i |
| B ←— 2 | 1 | 2 | n.i | n.i |
| C ←— 3 | 1 | 2 | 3 | n.i |
| D ←— A | 1 | 2 | 3 | 1 |
| A ←— C + 1 | 4 | 2 | 3 | 1 |
| B ←— D + C | 4 | 4 | 3 | 1 |
| C ←— D + 2 * A | 4 | 4 | 9 | 1 |
n.i signifie ici non initialisée. Une variable est non initialisée si aucune valeur ne lui a été explicitement affectée. A ←— 1 modifie la valeur contenue dans la variable A. A ce moment-là de l’exécution, les valeurs des autres variables sont inchangées. B ←— 2 modifie la valeur de B, les deux variables A et B sont maintenant initialisées. C ←— 3 et D ←— A initialisent les deux variables C et D, maintenant toutes les variables sont initialisées. Vous remarquerez que D a été initialisée avec la valeur de A, comme A est une variable initialisée, cela a un sens. Par contre, si l’on avait affecté à D le contenu d’une variable non initialisée, nous aurions exécuté une instruction qui n’a pas de sens. Vous noterez donc qu’il est interdit de faire figurer du coté droit d’une affectation une variable non initialisée. Vous remarquez que l’instruction D ←— A affecte à D la valeur de A, et que l’affectation A ←— C + 1 n’a pas de conséquence sur la variable D. Les deux variables A et D correspondent à deux emplacements distincts de la mémoire, modifier l’une n’affecte pas l’autre.
Un littéral est la représentation de la valeur d’une variable. Il s’agit de la façon dont on écrit les valeurs des variables directement dans l’algorithme.
Attention, 01 et 1 représentent les mêmes valeurs numériques, alors que "01" et "1" sont des valeurs alphanumériques distinctes. Nous avons vu dans l’exemple précédent des littéraux de type numérique, dans la section suivante il y a un exemple d’utilisation d’un variable de type alphanumérique.
Afin que nous soyons certains de bien nous comprendre lorsque nous rédigeons des algorithmes, définissons de façon précise des règles d’écriture. Un algorithme s’écrit en trois parties :
Par exemple,

La lisibilité des algorithmes est un critère de qualité prépondérant. Un algorithme correct mais indéchiffrable est aussi efficace qu’un algorithme faux. Donc c’est un algorithme faux. Vous devrez par conséquent soigner particulièrement vos algorithmes, ils doivent être faciles à lire, et rédigés de sorte qu’un lecteur soit non seulement capable de l’exécuter, mais aussi capable de le comprendre rapidement.
De nombreux algorithmes ont pour but de communiquer avec un utilisateur, cela se fait dans les deux sens, les sorties sont des envois de messages à l’utilisateur, les entrées sont des informations fournies par l’utilisateur.
Il est possible de demander à un utilisateur du programme de saisir une valeur :

La saisie interrompt le programme jusqu’à ce que l’utilisateur ait saisi une valeur au clavier. Une fois cela fait, la valeur saisie est placée dans la variable nomvariable. Il est possible de saisir plusieurs variables à la suite,

place trois valeurs saisies par l’utilisateur dans les variables A, B et C.
Pour afficher un message à destination de l’utilisateur, on se sert de la commande

Cette instruction affiche le <message> à l’utilisateur. Par exemple,

affiche "Hello World" (les guillemets sont très importantes !). Il est aussi possible d’afficher le contenu d’une variable,

affiche l’écran le contenu de la variable A. On peut entremêler les messages et les valeurs des variables. Par exemple, les instructions
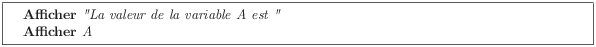
ont le même effet que l’instruction
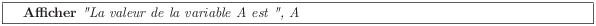
Lorsque l’on combine messages et variables dans les instruction d’affichage, on les sépare par des virgules. Notez bien que ce qui est délimité par des guillemets est affiché tel quel, alors tout ce qui n’est pas délimité par des guillemets est considéré comme des variables.
Cet algorithme demande à l’utilisateur de saisir une valeur numérique, ensuite il affiche la valeur saisie puis la même valeur incrémentée de 1.

Nous mettrons maintenant de côté le type numérique pour privilégier les deux types suivants :
Nous affinerons aussi les types alphanumériques en leur substituant les deux types suivants :
Les littéraux de type caractères seront délimités par des simples quotes (apostrophes) et les chaînes de caractères seront délimitées par des double-quotes (guillemets).
Le logiciel algobox permet de tester les algorithmes. Vous êtes invités à vous le procurer sur le site d’algobox.