Il est fréquent que l'on ne parvienne pas à exprimer ![]() en fonction
de
en fonction
de ![]() et de
et de ![]() , certaines récurrences sont très difficile à
résoudre. Une autre façon de classifier une suite
, certaines récurrences sont très difficile à
résoudre. Une autre façon de classifier une suite ![]() dans un
dans un
![]() est de conjecturer ce
est de conjecturer ce ![]() , puis de le
démontrer par récurrence. Par exemple, démontrons par récurrence que
, puis de le
démontrer par récurrence. Par exemple, démontrons par récurrence que
![]() . Si c'est le cas, supposons que
. Si c'est le cas, supposons que ![]() est
majorée par une suite linéaire, c'est à dire de la forme
est
majorée par une suite linéaire, c'est à dire de la forme ![]() . Choisissons
. Choisissons ![]() tel que
tel que
![]() et
et ![]() .
.
On montre aisément que ![]() et
et ![]() choisis conformément aux conditions
précédant la démonstration par récurrence détermine une suite
choisis conformément aux conditions
précédant la démonstration par récurrence détermine une suite ![]() qui majore
qui majore ![]() . On remarque que
. On remarque que ![]() croît de façon linéaire, en
effet
croît de façon linéaire, en
effet
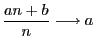 , donc on a
, donc on a
![]() . Comme
. Comme ![]() est majorée par une suite
linéaire,
est majorée par une suite
linéaire,
![]() .
.
Prouvons pour le sport que si ![]() et
et
![]() , alors
, alors
![]() . Comme
. Comme
![]() , alors
, alors
![]() , comme
, comme ![]() , alors pour les mêmes valeurs
, alors pour les mêmes valeurs
![]() et
et ![]() ,
,
![]() et de ce fait
et de ce fait
![]() .
.
Deux ensembles de méthodes ressortent dans les exemples :