



suivant: Listes chaînées
monter: Itérateurs
précédent: Exercice 6 - Itérateurs
Table des matières
- Soit
![$\left[ \begin{array}{l}F_n \\ F_{n-1}\end{array}\right] $](img260.gif) , un
vecteur de deux nombres de fibonacci consécutifs. Que donne le
produit
, un
vecteur de deux nombres de fibonacci consécutifs. Que donne le
produit
![$\left[ \begin{array}{l l}1 & 1 \\ 1 & 0 \end{array}\right]
\left[ \begin{array}{l}F_n \\ F_{n-1}\end{array}\right] $](img261.gif) ?
?
- Prouvez par récurrence que
![$\left[ \begin{array}{l l}1 & 1 \\ 1 & 0
\end{array}\right]^n \left[ \begin{arr...
...\end{array}\right] = \left[ \begin{array}{l}F_{n+1} \\
F_n\end{array}\right] $](img262.gif) .
.
- On calcule donc le
 -ème nombre de Fibonacci en mettant
préalablement la matrice
-ème nombre de Fibonacci en mettant
préalablement la matrice
![$\left[ \begin{array}{l l}1 & 1 \\ 1 & 0
\end{array}\right]$](img263.gif) à la puissance
à la puissance  . Nous allons utiliser pour
ce faire la même règle que pour
. Nous allons utiliser pour
ce faire la même règle que pour  . Ecrivez une
fonction
. Ecrivez une
fonction  prenant en paramètre deux quadruplets
prenant en paramètre deux quadruplets
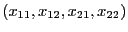 et
et
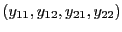 représentant deux matrices
représentant deux matrices
![$X
= \left[ \begin{array}{l l}x_{11} & x_{12} \\ x_{21} & x_{22}
\end{array}\right]$](img268.gif) et
et
![$Y
= \left[ \begin{array}{l l}y_{11} & y_{12} \\ y_{21} & y_{22}
\end{array}\right]$](img269.gif) .
.  retourne un quadruplet
représentant le produit matriciel
retourne un quadruplet
représentant le produit matriciel 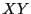 .
.
- Définir une fonction
 mettant un matrice
mettant un matrice  , à la
puissance
, à la
puissance  . Vous utiliserez
. Vous utiliserez
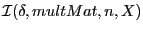 .
.
- Ecrire une fonction
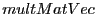 retournant le produit d'une
matrice, représentée par un quadruplet, et d'un vecteur, représenté
par un couple.
retournant le produit d'une
matrice, représentée par un quadruplet, et d'un vecteur, représenté
par un couple.
- Ecrire en C la fonction quadruplet applyFDQ(int (*delta)(int k),
unsigned long (*f)(int, quadruplet), int n, quadruplet x), vous
utiliserez le même modèle mathématique, mais en transmettant comme
deuxième paramètre à
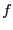 un quadruplet.
un quadruplet.
- Ecrire la fonction
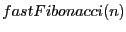 , retournant le
, retournant le  -ième nombre
de fibonacci.
-ième nombre
de fibonacci.
- Quelle est la complexité de
 ?
?
- Implémenter les fonctions :
- quadruplet multMat(quadruplet x, quadruplet y)
- quadruplet applyFDQ(unsigned long (*delta)(unsigned long),
quadruplet (*f)(unsigned long, quadruplet), unsigned long n,
quadruplet x
- quadruplet matPow(quadruplet x, unsigned long n)
- couple multMatVec(quadruplet x, couple y)
- unsigned long fastFibonacciIT(unsigned long l).




suivant: Listes chaînées
monter: Itérateurs
précédent: Exercice 6 - Itérateurs
Table des matières
klaus
2010-08-05
![$\left[ \begin{array}{l}F_n \\ F_{n-1}\end{array}\right] $](img260.gif) , un
vecteur de deux nombres de fibonacci consécutifs. Que donne le
produit
, un
vecteur de deux nombres de fibonacci consécutifs. Que donne le
produit
![$\left[ \begin{array}{l l}1 & 1 \\ 1 & 0 \end{array}\right]
\left[ \begin{array}{l}F_n \\ F_{n-1}\end{array}\right] $](img261.gif) ?
?
![$\left[ \begin{array}{l l}1 & 1 \\ 1 & 0
\end{array}\right]^n \left[ \begin{arr...
...\end{array}\right] = \left[ \begin{array}{l}F_{n+1} \\
F_n\end{array}\right] $](img262.gif) .
.
![$\left[ \begin{array}{l l}1 & 1 \\ 1 & 0
\end{array}\right]$](img263.gif) à la puissance
à la puissance ![$X
= \left[ \begin{array}{l l}x_{11} & x_{12} \\ x_{21} & x_{22}
\end{array}\right]$](img268.gif) et
et
![$Y
= \left[ \begin{array}{l l}y_{11} & y_{12} \\ y_{21} & y_{22}
\end{array}\right]$](img269.gif) .
.