



suivant: Exercice 7 - Itérateurs
monter: Itérateurs
précédent: Exercice 5 - Applications
Table des matières
Dans les questions précédentes, l'itérateur faisait décroître  de
de
 à chaque appel récursif. Soit
à chaque appel récursif. Soit 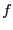 la fonction à itérer et
la fonction à itérer et 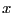 la
valeur en
la
valeur en 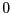 , nous pouvons définir un tel itérateur
, nous pouvons définir un tel itérateur  de
la sorte :
de
la sorte :
Nous étendons une telle fonction en ajoutant en paramètre une fonction
de décrément 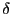 , on obtient :
, on obtient :
-

-
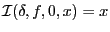 .
.
- Implémentez la fonction
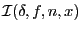 en en
utilisant le prototype suivant unsigned long applyFD(int
(*delta)(int k), unsigned long (*f)(couple), int n, unsigned long
x).
en en
utilisant le prototype suivant unsigned long applyFD(int
(*delta)(int k), unsigned long (*f)(couple), int n, unsigned long
x).
- Ecrivez une fonction
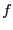 telle que
telle que
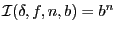 , vous utiliserez la relation de récurrence
, vous utiliserez la relation de récurrence
 et
et
 et poserez
et poserez
 .
.
- Prouvez que
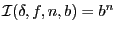
- Ecrivez en C la fonction unsigned long
slowPuissanceIT(unsigned long b, unsigned long n), vous
utiliserez applyFD et traduirez en C les fonctions
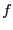 et
et
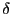 définies dans la question préccédente.
définies dans la question préccédente.
- Ecrivez deux fonctions
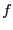 et
et 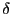 telles que
telles que

- Prouvez que

- Ecrivez en C la fonction unsigned long
fatorielleIT(unsigned long b, unsigned long n), vous
utiliserez applyFD.
- Ecrivez une fonction récursive
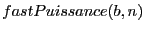 calculant
calculant  sans utiliser d'itérateur, vous utiliserez le fait que
sans utiliser d'itérateur, vous utiliserez le fait que
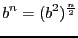 si
si  est pair et
est pair et
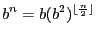 sinon.
sinon.
- Traduisez-là en C en utilisant le prototype suivant unsigned
long fastPuissance(unsigned long b, unsigned long n).
- Majorez le nombre d'appels récursifs en fonction de
 , est-ce
performant ?
, est-ce
performant ?
- Ecrivez la fonction
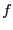 et la fonction
et la fonction 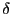 de sorte que
de sorte que
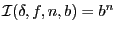 . Notez le fait que
. Notez le fait que 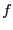 prend le
couple
prend le
couple  en paramètre.
en paramètre.
- Prouvez par récurrence la validité de
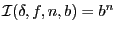 .
.
- Ecrivez en C la fonction unsigned long
fastPuissanceIT(unsigned long b, unsigned long n), vous
utiliserez la fonction applyFD.




suivant: Exercice 7 - Itérateurs
monter: Itérateurs
précédent: Exercice 5 - Applications
Table des matières
klaus
2010-08-05
![]() de
de
![]() à chaque appel récursif. Soit
à chaque appel récursif. Soit ![]() la fonction à itérer et
la fonction à itérer et ![]() la
valeur en
la
valeur en ![]() , nous pouvons définir un tel itérateur
, nous pouvons définir un tel itérateur ![]() de
la sorte :
de
la sorte :
![]() , on obtient :
, on obtient :