



suivant: Bibliographie
monter: Exercices récapitulatifs
précédent: Formule de Poincaré
Table des matières
Soient 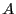 et
et  deux ensembles finis de cardinaux respectifs
deux ensembles finis de cardinaux respectifs 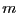 et
et
 .
.
- Combien existe-t-il de relations entre
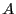 et
et  ? (Bijection avec
les parties de l'ensemble
? (Bijection avec
les parties de l'ensemble  )
)
- Combien existe-t-il d'applications de
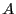 dans
dans  ? (Raisonnez par
récurrence)
? (Raisonnez par
récurrence)
- Combien existe-t-il d'applications bijectives de
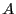 dans
dans  ?
(une bijection)
?
(une bijection)
- Combien existe-t-il de
 -uplets d'éléments de
-uplets d'éléments de 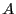 ?
(démerdez-vous)
?
(démerdez-vous)
- Combien existe-t-il de
 -uplets d'éléments distincts de
-uplets d'éléments distincts de 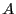 ?
?
- Combien existe-t-il d'applications injectives de
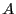 dans
dans  ?
(raisonnez par récurrence)
?
(raisonnez par récurrence)
- Combien existe-t-il de façon de partitionner un ensemble
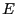 de
cardinal
de
cardinal  en
en 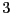 sous-ensembles ? C'est-à-dire de déterminer
sous-ensembles ? C'est-à-dire de déterminer 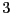 ensembles
ensembles 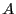 ,
,  et
et 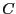 tels que
tels que
 ,
,
 ,
,
 et
et
 . (bijection)
. (bijection)
- Une application est croissante au sens large si
 . Combien existe-t-il
d'applications croissantes au sens large de
. Combien existe-t-il
d'applications croissantes au sens large de 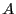 dans
dans  (supposés
ordonnés) ? (une bijection)
(supposés
ordonnés) ? (une bijection)
- Une application est croissante au sens strict si
 . Combien existe-t-il
d'applications croissantes au sens large de
. Combien existe-t-il
d'applications croissantes au sens large de 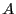 dans
dans  ? (plus
difficile, bijection...)
? (plus
difficile, bijection...)
- Combien existe-t-il de façon de partitionner un ensemble
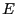 de
cardinal
de
cardinal  en
en 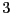 sous-ensembles non-vides ? (bijections
sous-ensembles non-vides ? (bijections  poincaré)
poincaré)
- Soit
 , un point fixe de
, un point fixe de 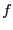 est un élément
est un élément
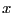 de
de 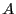 tel que
tel que  . Combien existe-t-il de bijection sans
point fixe ? (vraiment difficile, utilisez la formule de Poincaré
puis le binôme de Newton)
. Combien existe-t-il de bijection sans
point fixe ? (vraiment difficile, utilisez la formule de Poincaré
puis le binôme de Newton)




suivant: Bibliographie
monter: Exercices récapitulatifs
précédent: Formule de Poincaré
Table des matières
klaus
2010-08-05
![]() et
et ![]() deux ensembles finis de cardinaux respectifs
deux ensembles finis de cardinaux respectifs ![]() et
et
![]() .
.