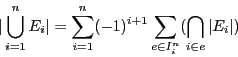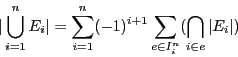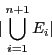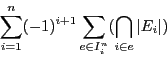suivant: La moulinette à méninges
monter: Exercices récapitulatifs
précédent: Echauffement
Table des matières
Le but de cet exercice est de prouver la formule de Poincaré :
En notant 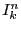 l'ensemble des sous-ensembles de
l'ensemble des sous-ensembles de
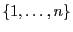 à
à  éléments, formellement :
éléments, formellement :
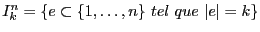
- Réecrivez la formule de Poincaré avec
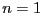
- Réecrivez la formule de Poincaré avec
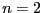
- Soient
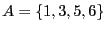 et
et
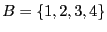 . Calculez
. Calculez
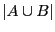 en utilisant la propriété
en utilisant la propriété
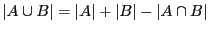 .
.
- Réecrivez la formule de Poincaré avec
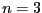
- Soit
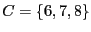 , utilisez la formule de Poincaré pour calculer
, utilisez la formule de Poincaré pour calculer
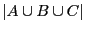 .
.
- On considère
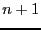 ensembles
ensembles
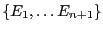 . Supposons la
formule de Poincaré vérifiée vérifiée au rang
. Supposons la
formule de Poincaré vérifiée vérifiée au rang  . Donnez alors une
relation entre
. Donnez alors une
relation entre
et
- Utilisez les résultats des questions précédentes pour prouver par
récurrence la formule de Poincaré.




suivant: La moulinette à méninges
monter: Exercices récapitulatifs
précédent: Echauffement
Table des matières
klaus
2010-08-05