On évite bon nombre de confusions en représentant sous forme d'arbre
les probabilités conditionnelles. Si par exemple ![]() ,
, ![]() et
et
![]() , on utilisera l'arbre de la
figure 1.1.
, on utilisera l'arbre de la
figure 1.1.
Cet arbre est un arbre de choix dans le sens où l'emprunt de chaque
branche correspond à un événement. Les deux branches partant de la
racine correspondent respectivement aux événements ![]() et
et ![]() ,
elles sont pondérées par
,
elles sont pondérées par ![]() et
et ![]() . Les deux branches
partant de
. Les deux branches
partant de ![]() sont étiquetées par
sont étiquetées par ![]() et
et ![]() et correspondent aux
événements
et correspondent aux
événements ![]() et
et ![]() . Elles dont pondérées par
. Elles dont pondérées par ![]() et
et
![]() . On calcule
. On calcule ![]() en multipliant les pondérations
des arêtes
en multipliant les pondérations
des arêtes ![]() et
et ![]() , donc
, donc
![]() . Le calcul de
. Le calcul de ![]() se fait en additionnant
se fait en additionnant
![]() et
et
![]() , donc
, donc ![]() . Il est aussi possible de représenter le même arbre plaçant
. Il est aussi possible de représenter le même arbre plaçant ![]() aux feuilles, pour cela il est nécessaire de connaître
aux feuilles, pour cela il est nécessaire de connaître
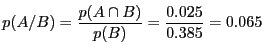 et
et
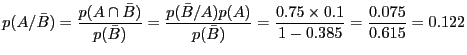 . On a donc :
. On a donc :
![\includegraphics[width=7cm]{chapitres/probas/arbre2.eps}](img174.png)