-
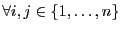 tels que
tels que 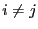 ,
,
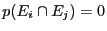 . (Tous les événements de
. (Tous les événements de 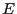 sont
incompatibles entre eux)
sont
incompatibles entre eux)
-
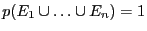 (Il y a toujours un
événement de
(Il y a toujours un
événement de 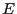 qui est réalisé)
qui est réalisé)
Autrement dit, ![]() est un système complet d'événements s'il y a
toujours un et un seul événement réalisé.
est un système complet d'événements s'il y a
toujours un et un seul événement réalisé.
Par exemple, soit ![]() un événement quelconque, alors
un événement quelconque, alors
![]() est un système complet d'événements, en effet
est un système complet d'événements, en effet ![]() et
et ![]() sont
incompatibles car
sont
incompatibles car
![]() et
et
![]() . Prenons comme autre exemple le lancer d'un dé, soit
. Prenons comme autre exemple le lancer d'un dé, soit ![]() l'événement "le dé tombe
sur la face
l'événement "le dé tombe
sur la face ![]() ", alors
", alors
![]() est un système complet
d'événements. En effet, considérons deux événements distincts
est un système complet
d'événements. En effet, considérons deux événements distincts ![]() et
et
![]() , comme il est impossible qu'un dé tombe sur deux faces
différentes lors du même lancer, alors
, comme il est impossible qu'un dé tombe sur deux faces
différentes lors du même lancer, alors
![]() . Comme un
dé tombe nécessairement sur une des faces, alors
. Comme un
dé tombe nécessairement sur une des faces, alors
![]() .
.
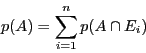
Considérons par exemple les événements ![]() et
et ![]() . Comme
. Comme
![]() forme un système complet d'événements avec
forme un système complet d'événements avec ![]() et
et ![]() , alors
, alors
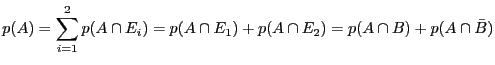 .
.