suivant : 1.7 Fonctions remonter : 1.6.3 Application à la précédent : 1.6.3.2 Matrice inverse

1.6.3.3 Systèmes d'équations

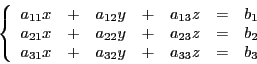
Etant donné un système d'équations de la forme :

$$\left \lbrace \begin{array}{l l l l l l l} a_{11}x & + & a_{... ...& + & a_{32}y & + & a_{33}z & = & b_{3} \\ \end{array}\right.$$

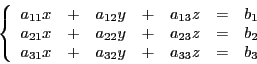
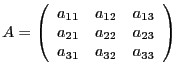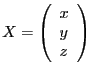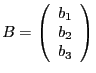Il est possible de réecrire le système sous forme matricielle : posons $A = \left(\begin{array}{l l l}a_{11}& a_{12}& a_{13}\\ a_{21} & a_{22} & a_{23} \\ a_{31}& a_{32}& a_{33}\end{array}\right)$, $X = \left(\begin{array}{l}x\\ y\\ z\end{array}\right)$ et $B = \left(\begin{array}{l}b_{1}\\ b_{2}\\ b_{3}\end{array}\right)$. Alors le système peut être écrit :

$$AX = B$$

Si la matrice $A$ est inversible, alors il existe $A^{-1}$ telle que $AA^{-1} = I$, prémultiplions alors les deux membres de l'équation matricielle précédente par $A^{-1}$, on a

$$A^{-1}AX = A^{-1}B$$

Comme $A^{-1}A = I$ et $IX = X$, alors l'équation précédente équivaut à

$$X = A^{-1}B$$

Cela signifie qu'on obtient la solution du système en multipliant le deuxième membre de l'équation par l'inverse de la matrice. Par conséquent, la connaissance de la matrice inverse de $A$ permet de résoudre ce système quel que soit le deuxième membre.

suivant : 1.7 Fonctions remonter : 1.6.3 Application à la précédent : 1.6.3.2 Matrice inverse