suivant : 1.5.2 Les systèmes triangulaires remonter : 1.5 Systèmes d'équations précédent : 1.5 Systèmes d'équations

1.5.1 Exemple

Vous disposez de trois matières premières $m_1$, $m_2$ et $m_3$ en stock dans une usine fabriquant des produits $p_1$, $p_2$ et $p_3$. Vous avez en stock $2000$ kilos de $m_1$, $3000$ kilos de $p_2$ et $2400$ kilos de $p_3$.

• Pour fabriquer un kilo de produit $p_1$, il faut $600$ grammes de $m_1$, $200$ grammes de $m_2$ et $200$ grammes de $m_3$.
• Pour fabriquer un kilo de produit $p_2$, il faut $200$ grammes de $m_1$, $700$ grammes de $m_2$ et $100$ grammes de $m_3$.
• Pour fabriquer un kilo de produit $p_3$, il faut $200$ grammes de $m_1$, $200$ grammes de $m_2$ et $600$ grammes de $m_3$.

Combien de kilos de $p_1$, de $p_2$ et de $p_3$ faut-il fabriquer pour vider les stocks ? Ce problème revient à résoudre un système de trois équations à trois inconnues. Soient $x$ la quantité de $p_1$ fabriquée, $y$ la quantité de $p_2$ fabriquée et $z$ la quantité de $p_3$ fabriquée. On représente la situation avec le système d'équations suivant :

$$\left \lbrace \begin{array}{l l l l l l l} 0.6x & + & 0.2y ... ... 0.2x & + & 0.1y & + & 0.6z & = & 2400\\ \end{array}\right.$$

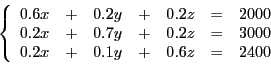
En déterminant les valeurs des inconnues $x$, $y$ et $z$ qui vérifieront simutanément les trois équations, nous aurons une solution au problème posé au début de l'exemple. Vous remarquez que tous les $x$ sont sur la même colonne, tous les $y$ aussi et de même pour les $z$. Cette convention de présentation permet de simplifier les calculs.

Dans cet exemple, on a comme solution $x = 1300$, $y=3040$ et $z=3060$. C'est assez simple à vérifier, mais la question que se pose probablement le lecteur, c'est comment on fait pour la trouver ?

suivant : 1.5.2 Les systèmes triangulaires remonter : 1.5 Systèmes d'équations précédent : 1.5 Systèmes d'équations