suivant : 1.4.2.3 Deux cas particuliers remonter : 1.4.2 Equations du premier précédent : 1.4.2.1 Qu'est-ce qu'une équation

1.4.2.2 Techniques de résolution

L'idée dégagée dans la section précédente, est que la méthode de résolution d'une équation est basée sur des réecritures successives d'une égalité avec des égalités équivalentes, interressons-nous donc à de telles méthodes.

• L'ajout d'une même valeur des deux cotés de l'égalité
• La multiplication des deux membres par une même valeur non nulle.

Considérons, à titre d'exemple, l'équation $x + 1 = 3$. Il va de soi que si l'on ajoute la même valeur des deux cotés de l'égalité, on obtiendra une équation équivalente (i.e. dont l'ensemble solution est le même). Par exemple, soustrayons $1$ (ce qui revient à additionner $-1$) à $x+1$ et à $3$, nous obtenons l'équation

$$x + 1 - 1 = 3 - 1$$

Ce qui se réecrit

$$x = 2$$

Nous aurions pu écrire, en rédigeant en façon très détaillée :

$$\begin{array}{l l l l} &x + 1 & = & 3 \\ \iff & x + 1 - 1 & = & 3 - 1 \\ \iff & x & = & 2\\ \iff & x \in \{2\} \end{array}$$

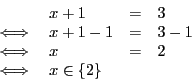
Remarquez que la méthode ci-dessus est une transposition quelque peu détaillée. Une transposition se rédige en n'écrivant pas le $+ 1 - 1$, on a ainsi non pas l'impression que $-1$ a été ajouté à chaque membre, mais que le $1$ du membre de gauche a été deplacé dans le membre de droite et transformé en $-1$.

$$\begin{array}{l l l l} &x + 1 & = & 3 \\ \iff & x & = & 3 - 1 \\ \iff & x & = & 2\\ \iff & x \in \{2\} \end{array}$$

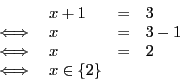
Remarquez aussi qu'une résolution se rédige en écrivant les équations les unes au dessus des autres. Les ''$\iff$'' servent à préciser le fait que toutes ces équations sont équivalentes.

Penchons-nous maintenant sur la deuxième méthode : la multiplication des deux membres par la même valeur non nulle. Vous aurez sûrement remarqué avec quelle zèle je m'acharne à écrire non nulle, j'insisterai lourdement sur cet aspect après avoir exposé la méthode.

Etant donné une équation, par exemple, $2x = 4$. Vous conviendrez qu'en multipliant les deux membres de cette équation par $\frac{1}{2}$, on obtiendra une égalité équivalente. On a

$$\frac{1}{2}2x = \frac{1}{2}4$$

Ce qui se réecrit

$$x = 2$$

Nous avons donc

$$\begin{array}{l l l l} &2x& = & 4 \\ \iff & \frac{1}{2}2x &... ...c{1}{2}4\\ \iff & x & = & 2\\ \iff & x \in \{2\} \end{array}$$

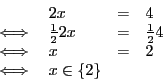
En règle générale, on n'écrit pas le $\frac{1}{2}2$. Ce qui donne l'impression que le $2$, est déplacé dans le membre de gauche puis inversé. Ce qui se rédige,

$$\begin{array}{l l l l} &2x& = & 4 \\ \iff & x & = & \frac{1}{2}4\\ \iff & x & = & 2\\ \iff & x \in \{2\} \end{array}$$

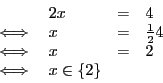
Approndissons les notions évoquées ci-dessus, nous souhaiterions pouvoir aditionner aux deux membres d'une équation la même expression, même si elle contient l'inconnue. Par exemple, pouvons-nous ajouter $x$ de part et d'autre de l'égalité $2x + 1 = - x$ ? La réponse est oui, on obtient

$$\begin{array}{l l l l} &2x + 1& = & - x \\ \iff & 2x + 1 + x & = & - x + x\\ \iff & 3x + 1 & = & 0\\ \end{array}$$

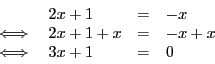
Nous souhaiterions, de façon analogue, pouvoir multiplier les deux membres d'une équation par une expression contenant l'inconnue. Là, par contre, se présente des problèmes fort délicats, par exemple,

$$\begin{array}{l l l l} &0& = & 1 \\ \iff & x \times 0 & = & x \times 1\\ \iff & 0 & = & x\\ \end{array}$$

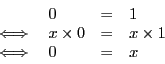
Vous constatez qu'en partant d'une relation fausse, nous retrouvons avec une solution. Que s'est-il passé ? Nous avons multiplié les deux membres de l'équation $0 = 1$ par une inconnue, qui comme son nom l'indique est inconnue. Cela signifie qu'on ne connait pas sa valeur, et que donc l'inconnue peut être nulle ! Il faut donc, lorsque vous multipliez les deux membres d'une équation par une expression dont vous ne connaissez pas la valeur, vous assurer qu'aucune valeur de l'inconnue ne peut annuler cette expression. Nous affinerons cette notion ultérieurement, notament dans les raisonnements par cas.

suivant : 1.4.2.3 Deux cas particuliers remonter : 1.4.2 Equations du premier précédent : 1.4.2.1 Qu'est-ce qu'une équation