Observons que si ![]() suit
suit
![]() , alors
, alors
dite aussi, loi normale centrée (de moyenne ![]() ) réduite (d'écart-ype
) réduite (d'écart-ype
![]() ). La fonction de répartition de la loi normale centrée réduite est
difficile à calculer manuellement. Il est d'usage d'utiliser soit des
logiciels, soit des tableaux. Les tableaux donnent les valeurs de la
fonction de répartition
). La fonction de répartition de la loi normale centrée réduite est
difficile à calculer manuellement. Il est d'usage d'utiliser soit des
logiciels, soit des tableaux. Les tableaux donnent les valeurs de la
fonction de répartition ![]() de la loi normale centrée réduite pour
de la loi normale centrée réduite pour
![]() strictement positif, on se ramène à une lecture de valeurs du
tableau avec les propriétés suivantes :
strictement positif, on se ramène à une lecture de valeurs du
tableau avec les propriétés suivantes :
Soit ![]() une variable aléatoire suivant
une variable aléatoire suivant
![]() ,
alors la variable aléatoire
,
alors la variable aléatoire
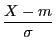 suit
une loi normale centrée réduite. On ramène donc le calcul de
suit
une loi normale centrée réduite. On ramène donc le calcul de ![]() à celui de
à celui de
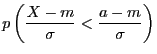 .
.