



suivant : 1.19.4 Opérations entre variables
remonter : 1.19 Variables aléatoires
précédent : 1.19.2 Espérance mathématique
Définition 1.19.5
Soit 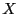 une variable aléatoire, alors la variance de
une variable aléatoire, alors la variance de 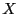 ,
notée
,
notée 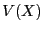 , est définie comme suit :
, est définie comme suit :
Dans l'exemple, on a
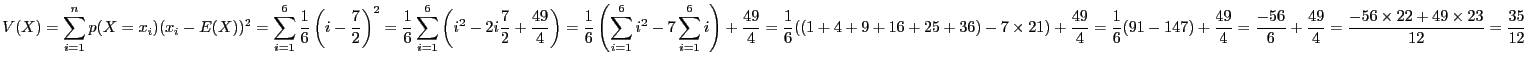 .
.
Définition 1.19.6
Soit 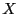 une variable aléatoire, alors l'écart-type de
une variable aléatoire, alors l'écart-type de 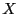 ,
noté
,
noté 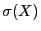 , est défini comme suit :
, est défini comme suit :
Propriété 1.19.1
Soit 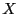 une variable alors
une variable alors
Pour simplifier la démonstration, nous noterons 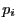 à la place de
à la place de
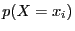 .
Par définition, on a
.
Par définition, on a
D'une part on a pour tout 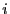 ,
,
Donc,
De plus,
Donc,
Décomposons la somme,
Mettons 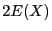 en facteur dans
en facteur dans
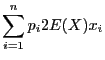 ,
,
Comme
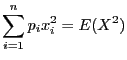 et
et
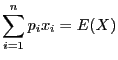 , alors
, alors
Comme
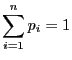 , alors
, alors
Ce qui se simplifie
Vérifions ce résultat sur l'exemple,
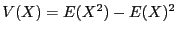 avec
avec
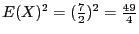 et
et
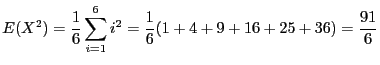 , donc
, donc
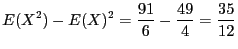 .
.




suivant : 1.19.4 Opérations entre variables
remonter : 1.19 Variables aléatoires
précédent : 1.19.2 Espérance mathématique
klaus
2011-02-14
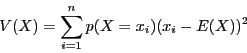
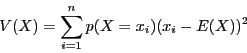
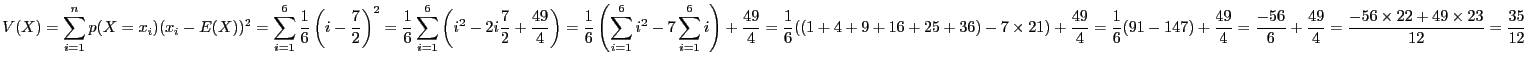 .
.
![]() à la place de
à la place de
![]() .
Par définition, on a
.
Par définition, on a
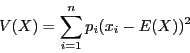
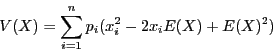
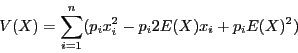
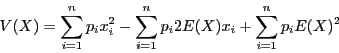
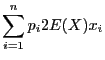 ,
,
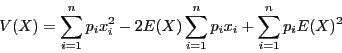
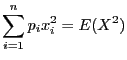 et
et
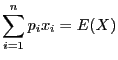 , alors
, alors
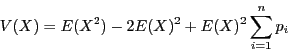
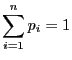 , alors
, alors
![]() avec
avec
![]() et
et
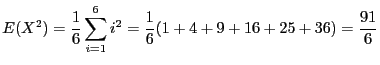 , donc
, donc
![]() .
.