



suivant : 1.16.5 Raisonnement par récurrence
remonter : 1.16 Suites numériques
précédent : 1.16.3 Suites géométriques
Définition 1.16.5
Soit 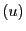 une suite numérique de premier terme
une suite numérique de premier terme 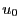 ,
,
- s'il existe
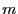 tel que tout
tel que tout 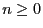 ,
, 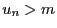 , alors
, alors 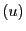 est minorée.
est minorée.
- s'il existe
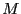 tel que tout
tel que tout 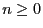 ,
, 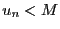 , alors
, alors 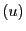 est majorée.
est majorée.
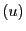 est bornée si elle est minorée et majorée.
est bornée si elle est minorée et majorée.
Théorème 1.16.1
Toute suite minorée et décroissante est convergente. Toute suite
majorée et croissante est convergente. Toute suite monotone et bornée
est couvergente.




suivant : 1.16.5 Raisonnement par récurrence
remonter : 1.16 Suites numériques
précédent : 1.16.3 Suites géométriques
klaus
2011-02-14
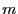 tel que tout
tel que tout 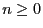 ,
, 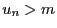 , alors
, alors 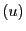 est minorée.
est minorée.
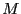 tel que tout
tel que tout 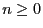 ,
, 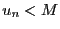 , alors
, alors 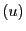 est majorée.
est majorée.
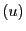 est bornée si elle est minorée et majorée.
est bornée si elle est minorée et majorée.