



suivant : 1.7.5 Parité
remonter : 1.7.4 Fonctions composées
précédent : 1.7.4.1 Domaine de définition
-
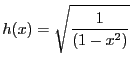 ,
on pose
,
on pose
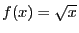 et
et
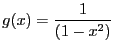 , on remarque que
, on remarque que 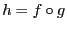 . Calculons
. Calculons 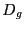 ,
,
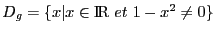 , or
, or
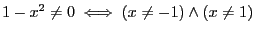 , donc
, donc
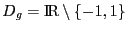 . On sait que
. On sait que
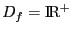 ,
définissons donc l'ensemble
,
définissons donc l'ensemble
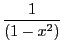 est du signe de
est du signe de
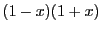 , qui est
strictement positif
, qui est
strictement positif
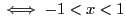 (si vous ne me croyez
pas, faites un tableau de signe !) et jamais nul car
(si vous ne me croyez
pas, faites un tableau de signe !) et jamais nul car
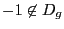 et
et 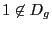 . Donc
. Donc
![$\displaystyle
\left\lbrace x \vert \frac{1}{(1 - x^2)} \geq 0 \right\rbrace = ]
-1, 1[$](img452.png) . Comme
. Comme
![$D_{g \circ f} = (\mbox{I\hspace{-.15em}R}\setminus \{-1, 1\})
\cap ] - 1, 1[ = ]-1, 1[$](img453.png) , on a finalement
, on a finalement
-
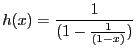 , on
pose
, on
pose
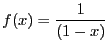 , on remarque que
, on remarque que
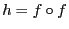 . On sait que
. On sait que
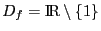 . Déterminons
maintenant
. Déterminons
maintenant
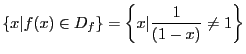 , on a
, on a
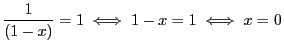 . Donc
. Donc
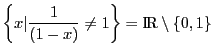 et on a
et on a
klaus
2011-02-14
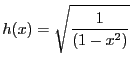 ,
on pose
,
on pose
![$\displaystyle
\left\lbrace x \vert \frac{1}{(1 - x^2)} \geq 0 \right\rbrace = ]
-1, 1[$](img452.png) . Comme
. Comme
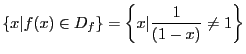 , on a
, on a
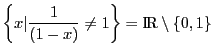 et on a
et on a
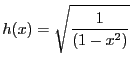 ,
on pose
,
on pose
![$\displaystyle
\left\lbrace x \vert \frac{1}{(1 - x^2)} \geq 0 \right\rbrace = ]
-1, 1[$](img452.png) . Comme
. Comme
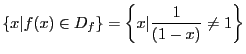 , on a
, on a
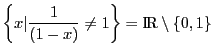 et on a
et on a