suivant : 1.4.3.2 Equations de degré remonter : 1.4.3 Factorisations précédent : 1.4.3 Factorisations

1.4.3.1 Un cas particulier

Considérons l'équation suivante :

$$(x + 1)(x + 2) = 0$$

Le membre de gauche est un produit, et les solutions de l'équation sont les valeurs de l'inconnue qui annulent ce produit. Les expressions qui sont multipliées s'appellent des facteurs, le premier membre de cette équation est un produit de facteurs.

On remarque que si on a $x = -1$, on a bien $(- 1 + 1)(- 1 + 2) = 0$. Il faut et il suffit que l'un des facteurs soit nul pour que le produit de facteurs soit nul. Ce type d'équation est très simple à résoudre, il suffit de décomposer cette équation en une disjonction de $2$ équations, on le rédige de la sorte :

$$\begin{array}{l l l l l l l l} &&&(x + 1)(x + 2)& = & 0 \\ ... ... -1 & ou & x & = & -2\\ \iff & x \in \{-1, -2\}\\ \end{array}$$

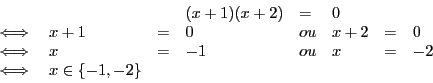
Comme les deux équations sont de degré $1$, elles sont de ce fait faciles à résoudre. Vous remarquez aussi que l'ensemble solution de $(x + 1)(x + 2) = 0$ est l'union des ensembles solution des deux équations $x + 1 = 0$ et $x + 2 = 0$.

suivant : 1.4.3.2 Equations de degré remonter : 1.4.3 Factorisations précédent : 1.4.3 Factorisations