



suivant : 1.4.2.2 Techniques de résolution
remonter : 1.4.2 Equations du premier
précédent : 1.4.2 Equations du premier
Une équation est une proposition liant des objets
mathématiques et faisant intervenir des inconnues. Par
exemple, 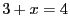 , la relation est dans cet exemple une égalité,
l'inconnue est
, la relation est dans cet exemple une égalité,
l'inconnue est 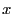 . Les objets additionnés sont appelés des
termes. Les termes se trouvant à gauche de l'égalité forment
le membre de gauche, dit aussi premier membre. Les
termes se trouvant à droite de l'égalité forment le membre de
droite, dit aussi deuxième membre.
. Les objets additionnés sont appelés des
termes. Les termes se trouvant à gauche de l'égalité forment
le membre de gauche, dit aussi premier membre. Les
termes se trouvant à droite de l'égalité forment le membre de
droite, dit aussi deuxième membre.
Une valeur est une solution de l'équation
si la relation est vérifiée quand on substitue cette valeur à
l'inconnue. Par exemple, 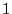 est une solution de l'équation
est une solution de l'équation
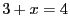 .
.
Une équation peut avoir plusieurs solutions, par exemple
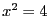 a pour solutions
a pour solutions 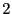 et
et 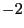 . On apelle ensemble
solution l'ensemble de toutes les solutions d'une
équation. Par exemple, l'ensemble solution de
. On apelle ensemble
solution l'ensemble de toutes les solutions d'une
équation. Par exemple, l'ensemble solution de 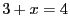 est
est 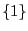 ,
l'ensemble solution de
,
l'ensemble solution de 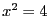 est
est 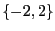 .
.
Il usuel de considérer une équation comme un prédicat, on dit alors
que deux équations sont équivalentes si elles ont le même
ensemble solution. Par exemple,
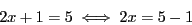
L'opération, appelée transposition, consistant à faire passer un
terme de l'autre coté de l'égalité en changeant son signe, permet de
changer l'écriture d'une équation sans changer son ensemble
solution. La résolution se fera en applicant successivement des
telles opérations jusqu'à ce que la solution se présente de façon
triviale. Par exemple,
Les étapes intermédiaires ont été volontairement occultées,
l'important ici est de saisir que l'on avait au début un relation non
triviale, et que l'on termine avec une relation qui donne de façon
explicite la solution de l'équation. De sorte qu'il est possible
d'écrire :
Autre exemple,
Bref, résoudre une équation 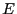 (qui est en fait un prédicat) revient
à déterminer un ensemble
(qui est en fait un prédicat) revient
à déterminer un ensemble 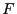 défini comme suit :
défini comme suit : 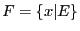 ,
c'est-à-dire l'ensemble des
,
c'est-à-dire l'ensemble des 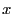 vérifiant la relation
vérifiant la relation 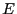 . Par
exemple,
. Par
exemple,
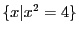 est l'ensemble des solutions de l'équation
est l'ensemble des solutions de l'équation
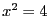 .
.
Il est possible, qu'après des réecritures vous parveniez à montrer
qu'une équation équivaut à une proposition toujours vraie, ou toujours
fausse. Si une équation équivaut à ''vrai'', alors toute valeur est
solution de cette équation. Si une équation équivaut à ''faux'', alors
aucune valeur n'est solution de cette équation.




suivant : 1.4.2.2 Techniques de résolution
remonter : 1.4.2 Equations du premier
précédent : 1.4.2 Equations du premier
klaus
2011-02-14