



suivant : 2.7 Fonctions
remonter : 2.6.4 Morceaux choisis
précédent : Exercice 13 - Transposée
Soient 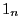 la matrice à
la matrice à 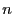 lignes et
lignes et 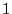 colonne ne contenant que
des
colonne ne contenant que
des 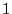 , et
, et 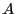 une matrice à
une matrice à 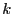 lignes et à
lignes et à 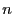 colonnes.
colonnes.
- Démontrez que pour tout
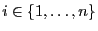 ,
, 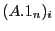 est la somme des éléments de la
est la somme des éléments de la 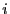 -ème ligne de
-ème ligne de
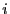 . (Revenez à la définition du produit matriciel)
. (Revenez à la définition du produit matriciel)
- Démontrer ensuite que
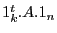 est une matrice
est une matrice
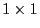 contenant la somme des éléments de
contenant la somme des éléments de 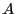 . (Utilisez la preuve
précédente)
. (Utilisez la preuve
précédente)
klaus
2011-02-14
![]() la matrice à
la matrice à ![]() lignes et
lignes et ![]() colonne ne contenant que
des
colonne ne contenant que
des ![]() , et
, et ![]() une matrice à
une matrice à ![]() lignes et à
lignes et à ![]() colonnes.
colonnes.