



suivant: Exercice 1 - Opérandes
monter: Preuves par induction
précédent: Lien avec les preuves
Table des matières
On veut démontrer que toute EATP contient au moins autant de
parenthèses que d'opérateurs. Procédons en ayant à l'esprit la
définition d'une EATP :
- Base
Les seules EATPs atomiques les expressions réduites à un réel, dont
ne contenant ni parenthèse, ni opérateur.
- Induction
Les quatre règles à considérer sont de la même forme :
 où
où  est un opérateur binaire,
est un opérateur binaire,  deux
EATPs, et
deux
EATPs, et 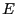 une EATP non atomique pour laquelle on cherche à
démontrer la propriété. Par hypothèse d'induction,
une EATP non atomique pour laquelle on cherche à
démontrer la propriété. Par hypothèse d'induction,  et
et  contiennent au moins autant de parenthèses que d'opérateurs. Et dans
l'expression
contiennent au moins autant de parenthèses que d'opérateurs. Et dans
l'expression  on ajoute plus de parenthèses que
d'opérateurs, donc
on ajoute plus de parenthèses que
d'opérateurs, donc 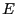 contient au moins autant de parenthèses que
d'opérateurs.
contient au moins autant de parenthèses que
d'opérateurs.
Sous-sections
klaus
2010-08-05